Komplexe Zahlen von kartesischer in Polarform umwandelt.

Question

Undzwar verstehe ich nicht wann ich (1) oder (2) anwenden muss (siehe Bild). Weil z.B −4 − 3j muss man um φ herauszufinden arctan (-3/-4) -180 rechnen also (2) 3.Quadranten anwenden) und bei z.B. − 3 − j  muss man um φ herauszufinden arctan (-1/-3) + 180 rechnen also (1) 3.Quadranten anwenden aber ich verstehe nicht wann ich (1) oder (2) anwenden muss...

Bild:

MfG

Answer 1

I. verwendest du, wenn du Winkel im Bereich 0 ≤ φ < 2pi haben möchtest.

II. verwendest du, wenn du Winkel im Bereich -pi < φ ≤ pi haben möchtest.

Achtung: ist ax = 0 dann kannst du den Winkel nicht über die Formel berechnen.

Comments

aber woher soll ich denn wissen welchen Winkel ich möchte? Weil in den Aufgaben steht bei uns immer nur z.B Polarkoordinaten gesucht

---

Wenn nichts angegeben ist dann kannst du frei wählen in welchem Bereich du den Winkel lieber hättest.

Rechnest du lieber mit -1/2*pi oder lieber mit 3/2*pi. Das liegt dann ganz an dir.

Answer 2

aber ich verstehe nicht wann ich (1) oder (2) anwenden muss...

Das steht eigentlich gerade neben (1) und (2).

Wenn positive Werte für phi verlangt sind, nimmst du (1).

Wenn Werte zwischen - π und π verlangt sind, nimmst du (2).

Comments

aber woher soll ich denn wissen welchen Winkel ich möchte? Weil in den Aufgaben steht bei uns immer nur z.B Polarkoordinaten gesucht

---

Du musst aus deinen Unterlagen / der Vorlesung wissen, ob ihr die Winkel in Polarkoordinaten zwischen 0 und 2π oder zwischen -π und π angeben müsst.

Answer 3

z= −4 − 3j → 3.Quadrant in der Gaußschen Zahlenebene

Es gilt allgemein:

tan(α) = Imaginärteil/Realteil =-3/-4

tan(α)=3/4

α ≈ 36.87° +180° ≈ 216.9°, damit Du in den 3. Quadranten kommst.

Answer 4

Hallo mistermathe,

wenn dir die Aufgabenstellung mal nicht den Gebrauch von tan aufzwingt (#):  

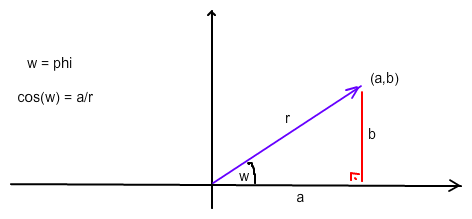
kartesische Form  a + b  · i     →   Polarform  r · e^φ·i

$$ r = \sqrt{a^2 +b^2}\text{ } \text{ }$$$$φ = arccos\left(\frac { a }{ r }\right) \text{ }\text{ } wenn \text{ }\text{ }b≥0 \text{ } \text{ } \text{ } \text{ } [ \text{ } - arccos\left(\frac { a }{ r }\right)\text{ }wenn \text{ }\text{ }b<0 \text{ } ] .$$Kann man sich ganz leicht merken:

b ≥0  →  + ...  ,   b<0  →  - ....   !

--------

#

Ich werde deshalb nie begreifen, warum hier fast jeder den tan anwenden will :-)

Gruß Wolfgang