Sämtliche Zahlen (z Element komplexer Zahlen) ermitteln

Question

Hallo User,

Aufgabenstellung: ermittelt sämtliche Zahlen (z Element komplexer Zahlen) für:

Aufg1) z^4=-16

Aufg2) z^3+3iz^2-3z-9i=0 Hinweis: kubische Ergänzung

Aufg3) z^2-3z+3-i=0

Leider sagt mir sowas überhaupt nichts, weshalb ich auch auf Google keine Ahnung habe wonach ich suchen soll.

Würde mich über Hilfe freuen. Danke.

Comments

https://www.google.de/search?&q=z^4%3D-16

Answer 1

3. Aufgabe:

z^2-3z+3-i=0 ->PQ-Formel

z_1.2= 3/2 ± √ ((-3)/4 +i)

z_1.2= 3/2 ±  1/2 +i

z₁= 1-i

z₂= 2+i

Comments

müsse es nicht -3/2 heißen und 9/4?

also die Lösung stimmt mit der aus meinen Notizen überein, bloss verstehe ich nicht wie du die Zahlen wählst..

---

ich habe eine Zeile weggelassen: (schon vorher zusammengefasst)

z^2-3z+3-i=0 ->PQ-Formel

z_1.2= 3/2± √ (9/4 -3 +i)
z_1.2= 3/2 ± √ ((-3)/4 +i)

---

ahh okay ich habe es verstanden. vielen lieben Dank.

---

jedoch eine letzte frage..

wurzel -3/4 kann man doch gar nicht auflösen, wie kommst du dann auf die 1/2?

---

Eine Möglichkeit:

Du wandelst den Term in die Exponentialform um.

Vorher ist der Betrag und Winkel zu bilden.

Answer 2

1) Substitution mit u=z²

ergibt leicht zu lösende pq-Formel, die auch mit komplexen Zahlen funktioniert

3) ist pq-Formel, die auch mit komplexen Zahlen funktioniert

2)

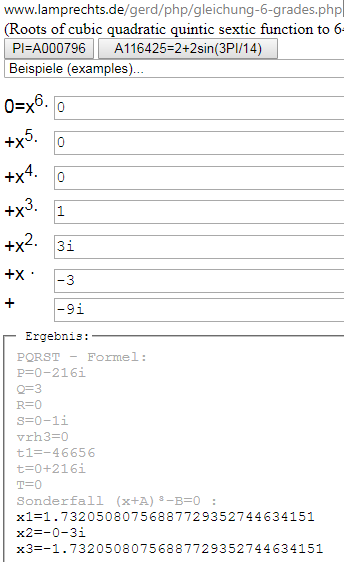
Lösung a) da PQRST-Formeln für kubische Gl.  nicht Lehrplan sind, stellen Lehrer nur Aufgaben, die man leicht erraten kann: bei -3i findet man leicht die erste Nullstelle

Dann durch diese geteilt (siehe Polynomdivision)

(z+3i)*(z²-3)=0 siehe auch "Satz vom Nullprodukt"

ergibt pq-Formel -> die auch mit komplexen Zahlen funktioniert also +/-sqrt(3)

Lösung b) PQRST-Formeln für kubische Gl.

http://www.lamprechts.de/gerd/php/gleichung-6-grades.php