Lösung der Aufgabe: (1-i )/ (2-i)

Question

(1-i )/ (2-i)

Ich würde gerne den Lösungsweg für diese Aufgabe kennen lernen.

Danke !

Answer 1

(1-i )/ (2-i)

Ich würde gerne den Lösungsweg für diese Aufgabe kennen lernen.

Bis jetzt ist keine Aufgabe zu erkennen ;)

(1-i )/ (2-i)  ist ein Bruch ähnlich wie 3/4, nur werden zwei komplexe Zahlen durcheinander geteilt. 

Was sollst du tun? Was ist gefragt?

Man könnte z.B. den Nenner reell machen. Da würde man dann standardmässig mit der 3. binomischen Formel erweitern.

[spoiler]

Also:

(1-i )/ (2-i)

= ( (1-i )/ (2-i) ) * ((2+i)/(2+i) )       | Bruchmultiplikation

= ((1-i)(2+i)) / ( 4 - i^2)

= ( 2 + i - 2i - i^2)/ ( 4 + 1)

= ( 2 - i + 1)/(5)

= (3 - i)/5 

[/spoiler]

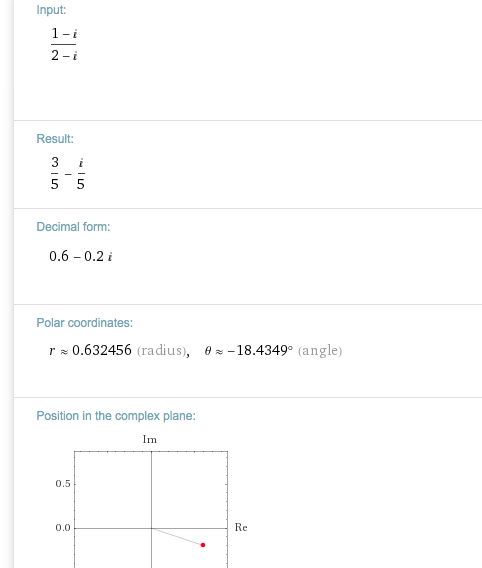
Du kannst den Bruch auch hier eingeben und schauen, was da sonst noch so alles berechnet werden könnte:

https://www.wolframalpha.com/input/?i=(1-i+)%2F+(2-i)

Comments

Danke für die schnelle Antwort!

---

Bitte. Was war denn nun gefragt?

Answer 2

Du mußt konjugiert komplex den Nenner und Zähler erweitern  mit  2+i

Answer 3

  Du weißt. das im Nenner nie eine  "  Wurzel  " stehen darf; und  i  ist doch weiter nix als  ein Beispiel für eine Wurzel.  Wie würdest di vorgehen, wenn da statt  i  stünde

        2  -  sqr ( 3 )

     -------------------------

        3  +  sqr  (  3  )