Aufgabe 2:
Untersuchungen zur Absatzentwicklung von zwei Konkurrenzunternehmen:
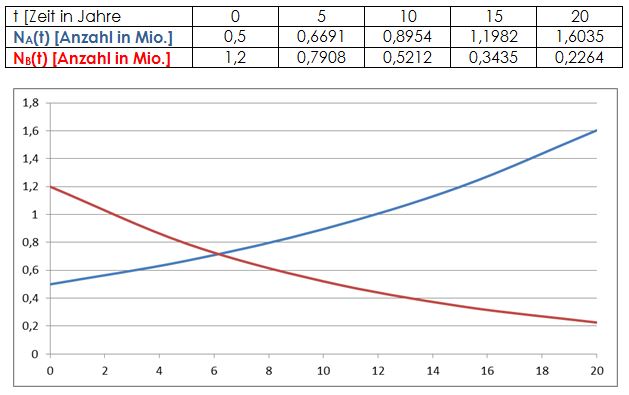
Firma A: Die Firma expandiert stark und erwartet jährliche Wachstumsraten von \( 6 \% \) mit der Wachstumsgleichung \( \mathrm{N}_{\mathrm{A}}(\mathrm{t})=0,5 \cdot 1,06^{+} \) \( \dagger[ \) Jahre], \( N \) [ME in Millionen].
Firma B: \( \quad \) Mit den innovativen Produkten von Firma \( \mathrm{A} \) kann diese Traditionsfirma nicht konkurrieren.
Der Absatz ist daher stark rückläufig und wird mit der Funktion \( \mathrm{N}_{\mathrm{B}}(\mathrm{t})=1,2 \cdot 0,92^{\text {t }} \) prognostiziert.
| t (Zeit in Jahren) | 0 | 5 | 10 | 15 | 20 |
| N_{A}(T) (Anzahl in Mio.) |
|
|
|
|
|
N_{B}(T) (Anzahl in Mio.)
|
|
|
|
|
|
2.1 Erklären Sie die Bedeutung der Wachstumsfaktoren \( \mathrm{q}_{\mathrm{A}}=1,06 \) und \( \mathrm{q}_{\mathrm{s}}=0,92 \)
2.2 Berechnen Sie die Daten für die Absatzentwicklung der Firmen (Wertetabelle). Veranschaulichen Sie die Absatzentwicklung in einem Diagramm.
2.3 Ab welchem Zeitpunkt ( \( t= \) ?) wird Firma A absatzmäBig zum Marktführer (Berechnungsgenauigkeit \( 10^{-2} \))?
2.4 Die momentane Wachstumsgeschwindigkeit (lokale Änderungsrate, Ableitung) ist als Grenzwert definiert. Geben Sie eine Definition dieses Grenzwertes an.
2.5 Zum Zeitpunkt \( t \approx 6,18 \) haben beide Firmen die gleiche Absatzmenge. Berechnen und vergleichen Sie die momentanen Änderungsraten (Wachstumsgeschwindigkeiten) zu diesem Zeitpunkt:
a) näherungsweise Berechnung mit \( \Delta t=0,01 \);
b) mit Hilfe von Ableitungsfunktionen
2.6 Zeigen Sie, dass für die Wachstumsfunktion \( \mathrm{N}_{\mathrm{B}} \) gilt: \( \mathrm{N}_{\mathrm{B}}^{\prime}(\mathrm{t})=\mathrm{k} \cdot \mathrm{N}_{\mathrm{B}}(\mathrm{t}) . \) Interpretieren Sie die Bedeutung dieser Gleichung.
Aufgabe 4:
Gegeben ist die Funktion \( f \) mit \( f(x)=e^{x} \cdot\left(2 x^{2}+2 x-4\right) D_{F}=[-6 ; 1] \)
4.1 Führen Sie eine sorgfältige Kurvendiskussion durch (Achsenabschnitt, Nullstellen, Extremstellen, Wendestellen).
4.2 Notieren Sie Ihre Ergebnisse übersichtlich in der Wertetabelle:
| Punktart (N, H, T, W) |
|
|
|
|
|
|
|
| x = |
|
|
|
|
|
|
|
| y = f(x) |
|
|
|
|
|
|
|
| m_{T} = f'(x) |
|
|
|
|
|
|
|
4.3 Konstruieren Sie den Graphen von \( f \) mit Hilfe berechneten Punkte (Tangenten zeichnen; Zeicheneinheiten für beide Achsen \( 2 \mathrm{~cm} \) ).
4.4 Gegeben ist die Funktion \( g \) mit \( g(x)=e x \cdot\left(x^{2}+a \cdot x+b\right) \). Bestimmen Sie a und b so, dass \( \mathrm{X}_{\mathrm{El}}=-2 \) und \( \mathrm{X}_{\mathrm{E} 2}=1 \) mögliche Extremstellen sind.
Lösung von Aufgabe 2.2: