Vektorrechnung, Punkt in Ebene bestimmen durch Senkrechte

Question

Heyhu Leute, ich stehe kurz vor meinem Abschluss und bin beim Wiederholen auf eine Aufgabe gestoßen, zu der ich keinen richtigen Ansatz finde.

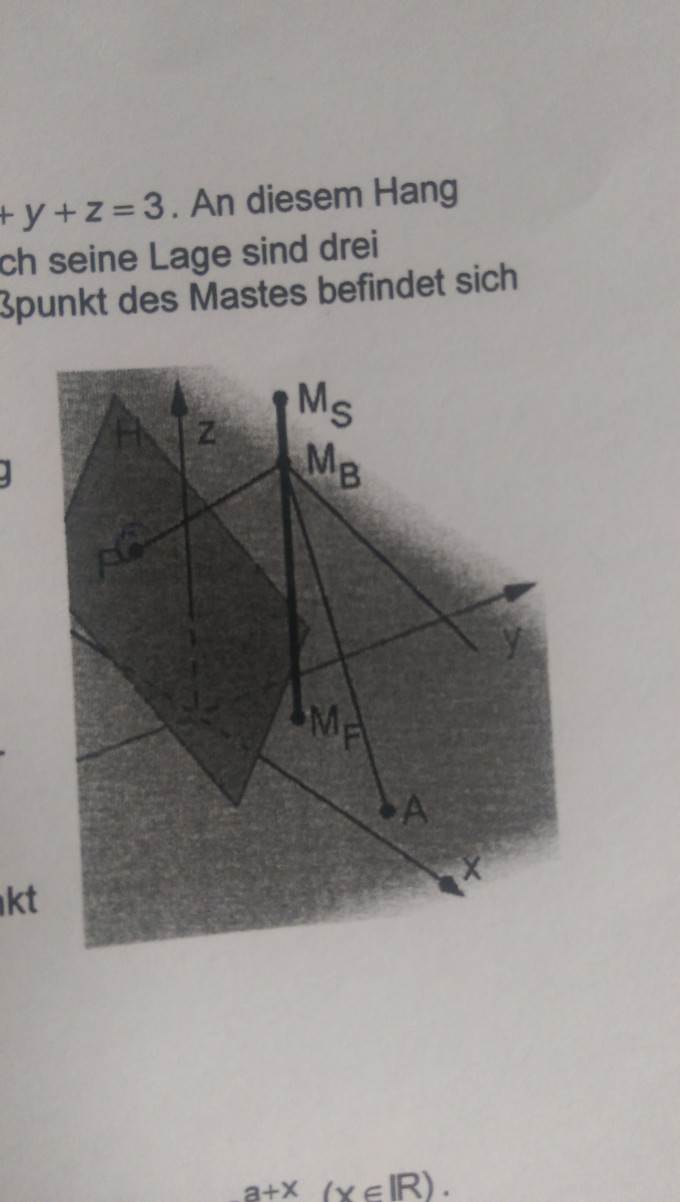
Die Lage eines Hanges ist gegeben durch die Ebenengleichung H: x+y+z=3. An diesem Hang soll für eine Telefonleitung ein senkrechter Mast errichtet werden. Durch seine Lage sind drei Abspannungen zur Befestigung und Stabilisierung notwendig. Der Fußpunkt des Mastes befindet sich in M_f(2|2|0).

Ein Abspannseil soll vom Befestigungspunkt M_b senkrecht zum Hang zum Punkt P verlaufen. Der Befestigungspunkt M_b liegt bei M_b(2|2|8).

Aufgabe: Bestimmen Sie die Koordinaten des Befestigungspunktes P der Abspannung.

                                                       1

Soweit das der Normalvektor n_e=  1   ,ist bin ich schon. Und das der Vektor

                                                       1

der senkrecht auf P steht parallel zum Normalvektor sein muss ist auch klar. Nur ich finde überhaupt keinen Ansatz wie ich weiter machen muss, ich wäre euch sehr dankbar wenn sich wer kurz Zeit nehmen würde :)

Answer 1

Hallo

 da die Ebene in Koordinatenform gegeben ist, kennt man einen Normalenvektor (1,1,1)

 das ist dann der Richtubgsvektor der Geraden längs der das Spannseil läuft. du musst also die ebene mit der Geraden mit Aufpunkt (2,2,8) und Richtungsvektor (1,1,1) schneiden,

aber viel einfacher: du normierst den Normalenvektor  auf n₀, dann hast du für die Ebene n₀*x=d bei dir d=√3,  dann ist der Abstand zu einem Punkt P mit Ortsvektor p

d(EP)=n₀*p-d

Gruß lul