Alternative viel kürzer und ohne Fallunterscheidung:
|x-4|<|x+2| | Quadrieren.
(x-4)^2 < (x+2)^2
x^2 - 8x + 16 < x^2 + 4x + 4
12 < 12x
1 < x
L = { x Elment R | 1 < x } fertig.
Nun eure Vorgaben:
Dazu soll man die 3 Fälle betrachten x ∈ (-∞,-2) , x ∈ [-2,4], x ∈ (4, ∞).
Habe wirklich viel Zeiut damit verbracht einen Lösungsansatz zu finden, so weit bin ich bis jetzt gekommen.
Wäre wirklich sehr dankbar wenn das jemand mal verständlich vorrechnen würde.
1. Fall x ∈ (-∞,-2) , d.h. x<-2.
|x-4| = 4-x ; |x+2| = -(2+x)
|x-4|<|x+2|
4 - x < -(2 + x)
4 - x < - 2 - x
4 < - 2 falsch! D.h. die Betragsgleichung ist für kein x < - 2 erfüllt.
Zweiter Fall: x ∈ [-2,4]
|x-4|-|x+2|<0
(4-x) - (2+x) <0
2 -2x <0 |-2
-2x < -2 | :-2
x > 1
Wenn du richtig gerechnet hast ist L1 = {x Element R | 1 < x ≤ 4}
3. Fall fehlt noch.
Danach die Teile der Lösungsmenge miteinander vereinen.
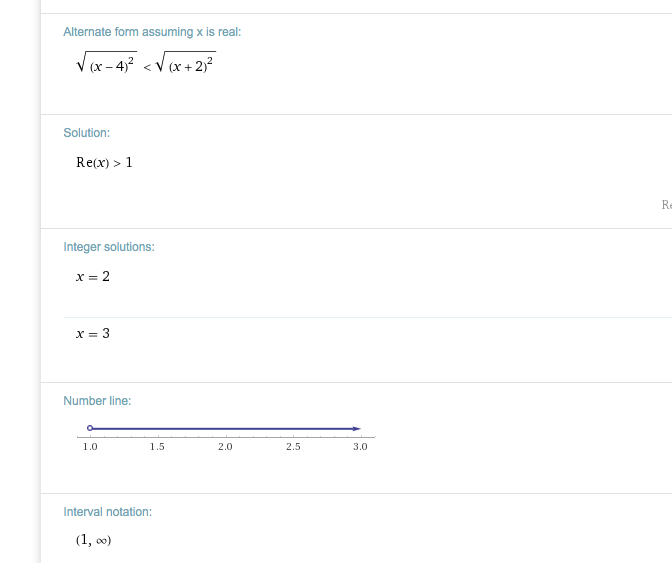
Zur Kontrolle:
https://www.wolframalpha.com/input/?i=%7Cx-4%7C%3C%7Cx%2B2%7C