Wenn Du die Länge bzw. den Betrag der Vektoren \(p\) und \(q\) berechnest, so erhältst Du:
$$\| p \| = \sqrt{ \sqrt{2}^2 + 1^2 + ^2 } = 2 \\ \| q\| = \sqrt{\left(\frac23 \sqrt{3}\right)^2 + \left(\frac23 \sqrt{2}\right)^2 + \left(\frac43 \right)^2} = \sqrt{\frac43 + \frac89 + \frac{16}{9}} = 2$$
Das heißt, die Punkte \(P\) und \(Q\) befinden sich auf der Obefläche einer Kugel mit Radius \(2\) deren Mittelpunkt im Ursprung liegt. Wie folgendes Bild zeigt:
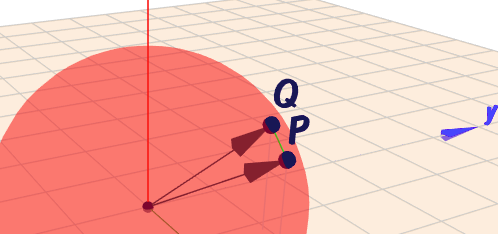
(klick auf das Bild)
Mit \(v = s \cdot p + (1-s) \cdot q; \space s \in [0;1]\) sind alle Vektoren gegeben, deren Endpunkte sich auf der Strecke zwischen \(P\) und \(Q\) befinden (kleine grüne Strecke im Bild). Da dies eine Sehne innerhalb der Kugel ist, muss offensichtlich für alle \(v\) gelten \(\|v\| \le 2\).
Rechnen kann man das aber auch:
$$\|v\| = \|s p + (1-s) q\| = \sqrt{s^2 p^2 + 2s(1-s)pq + (1-s)^2 q^2}$$
Jetzt gilt aber \(p^2=q^2=4\) und \(pq \lt 4\). Folglich ist
$$\sqrt{s^2 p^2 + 2s(1-s)pq + (1-s)^2 q^2} \le \sqrt{4(s^2 + 2s(1-s) + (1-s)^2 )}=2(s+(1-s)) = 2$$ q.e.d.
Bem.: die Ungleichung gilt genau dann, wenn \(2s (1-s)\ge 0\) ist. Das ist aber mit \(s \in [0;1]\) erfüllt.