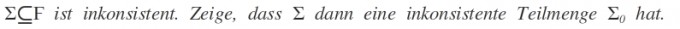
Σ⊆F ist inkonsistent, dann gibt es eine endliche Teilmenge Σ0 ⊆ Σ, die inkonsistent ist.
Mir fällt als erstes der Kompaktheitssatz ein, mit dem Korollar dass Sigma eine Formel A erfüllt, wenn eine Teilmenge von Sigma bereits A erfüllt.
Inkonsistent bedeutet, dass Sigma eine Formel A erfüllt, und gleichzeitig eine Formel ¬A erfüllt.
Wie kann ich diese Aussagen geschickt verbinden so dass ich zeigen kann, dass die Aussage gilt?