Kreis oder Linie? x^2 +y^2 ≤ 16

Question

x^2 +y^2 ≤ 16

Wie bekomme ich hieraus eine Kreisgleichung? Wenn ich beliebige Werte eingebe, dann ergibt sich bei eine Gerade. Laut unserem Lehrer soll es eine Kreisgleichung sein?!?

Wie geht das denn überhaupt, denn es kann ja nicht ins Negative aufgrund der Potenz....

Lg

Comments

Das ist die Koordinatenbeziehung einer Kreisscheibe mit Radius 4 um den Ursprung. Es ist eine Ungleichung.

Answer 1

x^2 + y^2 ≤ 16 Ist eine Kreisfläche

x^2 + y^2 = 16 wäre der Rand des Kreises.

Wir können mal nach y auflösen

y = ± √(16 - x^2)

Kannst du das selber mal skizzieren?

Comments

Ok, super! So hatˋs geklappt.

Und dann noch blöde Frage zum Abschluss: wieso heißt es +/- die Wurzel?! Ist es nicht ein positives Vorzeichen, solange es nicht klar als negativ deklariert ist?

---

 x² = 4  ⇔  x = 2  oder  x = -2

dafür schreibt man auch  x = ±2

genauso bei Wurzeln:

x² = 3  ⇔  x = √3  oder  x = - √3

dafür schreibt man auch  x = ± √3

Answer 2

x^2 +y^2 ≤ 16
nehmen wir einmal den äußersten Fall
x^2 +y^2 = 16
16 = x^2 + y^2
4^2 = x^2 + y^2
Dies ist der Pythagoras mit
4 als Hypotenuse
x,y als An- und Gegenkathete im rechtwinklingen
Dreieck.
Das Bild dieser Funktion ergibt einen Kreis.
Am Besten selbst einmal zeichnen mit
Hilfe einer Wertetabelle.

Comments

Auch hier: wie komme ich denn in den negativen x-Bereich? Durch das ^2 kann ja kann y nie negativ werden.

---

x^2 + y^2 ≤ 16

(-2)^2 + (- 3)^2 ≤ 16

Du siehst dass ich durchaus für x und y auch negative Werte einsetzen kann.

Answer 3

Mathematisch ist ein Kreis in der Zeichenebene die Menge der Punkte, die von einem gegebenen Punkt (Mittelpunkt M) den gleichen Abstand (Radius) haben. D.h. Kreis = Kreislinie.

Kreis und Pythagoras im Bild:

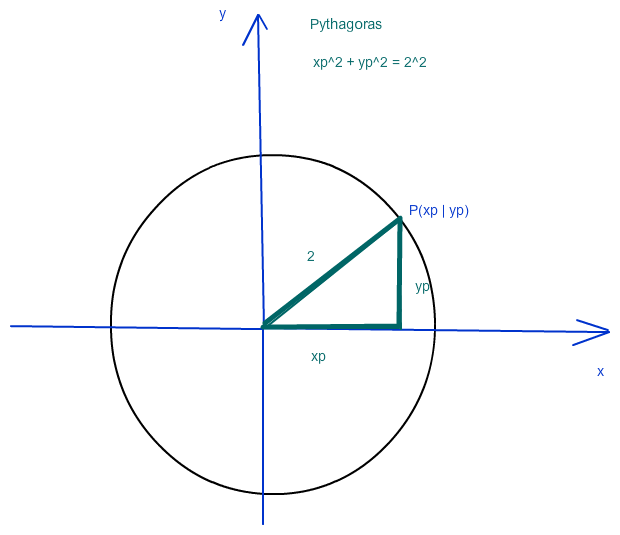
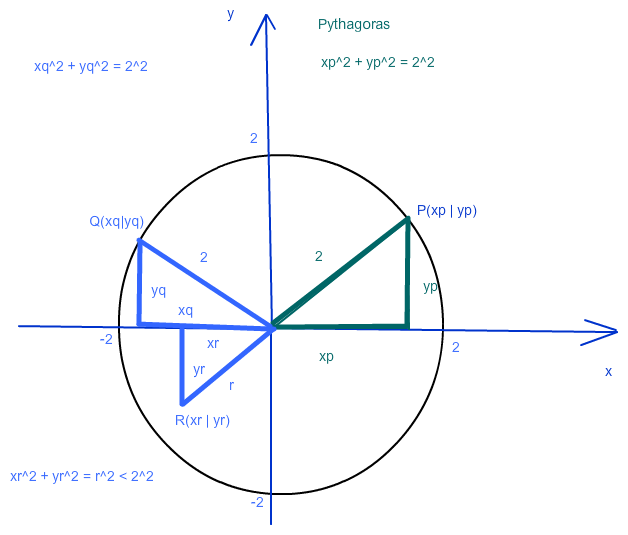
Wegen Pythagoras lautet die Kreisgleichung für die Zeichnung x^2 + y^2 = r^2 , x^2 + y^2 = 4

Sind alle Punkte der Kreisscheibe (Kreis und sein Inneres) gemeint, passt x^2 + y^2 ≤ 4 .