Ableiten mit Hilfe der Potenzregeln fk(x) = 2k / e^kx + e^-kx

Question

fk(x) = 2k / e^kx + e^-kx

Kann man das ganze umschreiben mt hilfer der Potenzregeln ?

Ich muss es ableiten und will es nicht mit der Qutientenregel machen sondern mit der Produktregel.

Comments

fk(x) = (2k / ekx) + e^-kx

Sollen die Klammern so gesetzt sein?

---

ich vermute einmal so
fk(x) = 2k / ( e ^{kx} + e ^{-kx} )

---

Falls noch Fragen sind dann wieder melden.

---

Ja richtig

 fk(x) = 2k / ( e^kx + 3^-kx)

Ich schreibe es einfach um, mit hilfe potenzregel dann wende ich kettenregel und Produktregel an danke :)

Answer 1

schreibe

f_(k)(x)=2k*(e^{kx}+e^{-kx})^{-1}

uns verwende Ketten und Produktregel. Das kann man hier im Kopf machen.

Answer 2

f_k(x) = (2k / e^kx) + e^{-kx}

= (2k * e^-kx+ e^{-kx}  = (2k+1)*e^{-kx} 

Answer 3

f ( x ) = 2k / ( e ^{kx} + e ^{-kx} )
f ( x ) = 2k *  ( e ^{kx} + e ^{-kx} ) ^{-1}
2k ist nur ein Faktor der beim Ableiten erhalten
bleibt
[ term ^{-1} ] ´ = (-1) * term ^{-2} * ( term )
term = e ^{kx} + e ^{-kx}
term ´ =  e ^{kx} * k   + e ^{-kx} * (-k) )
term ´ =  e ^{kx} * k  - e ^{-kx} * k
term ´ =  k * [ e ^{kx}  - e ^{-kx} ]

[ term ^{-1} ] ´ = (-1) * term ^{-2} * ( term )
[ term ^{-1} ] ´
= (-1) * term ^{-2} * ( k * [ e ^{kx}  - e ^{-kx} ] )
Insgesamt
- 2k * k * ( e ^{kx} + e ^{-kx} ) ^{-2}  * (e ^{kx}  - e ^{-kx})
- 2k^2 * ( e ^{kx} + e ^{-kx} ) ^{-2}  * (e ^{kx}  - e ^{-kx})

Matheprogramm

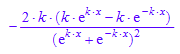
Ist dasselbe.