Extrempunkte und Graphen von f(x)= -x^3+20x^2 und k(x)=x^3 -13x^2+40x

Question

meine frage ist wie komme ich zur lösung der extremwerte dieser aufgabe?

f(x)=-x^3+20x^2

k(x)=x^3-13x^2+40x

und den graphen zu beiden skizzieren

ich habe schon eine vermutung  aber ich glaub nicht dass die stimmt weil es eine komisch grosse kommalösung ist.

Answer 1

Für f(x): x=9 1/3

Für k(x): x=6 2/3


Du bildest bei beiden jeweils die Ableitung und löst nach x auf.

Für k(x) brauchst du zusätzlich binomische Formeln.

Comments

aber wie sehen die den aus?

Answer 2

f(x) = - x^3 + 20·x^2
f'(x) = 40·x - 3·x^2
f''(x) = 40 - 6·x 

k(x) = x^3 - 13·x^2 + 40·x
k'(x) = 3·x^2 - 26·x + 40
k''(x) = 6·x - 26 

Extremstellen f'(x) = 0

40·x - 3·x^2 = 0
x = 40/3 ∨ x = 0

f''(40/3) = -40 --> Hochpunkt
f(40/3) = 32000/27 = 1185.185185

f''(0) = 40 --> Tiefpunkt
f(0) = 0

Extremstellen k'(x) = 0

3·x^2 - 26·x + 40 = 0
x = 20/3 ∨ x = 2

k''(20/3) = 14 --> Tiefpunkt
k(20/3) = - 400/27 = -14.81481481

k''(2) = -14 --> Hochpunkt
k(2) = 36

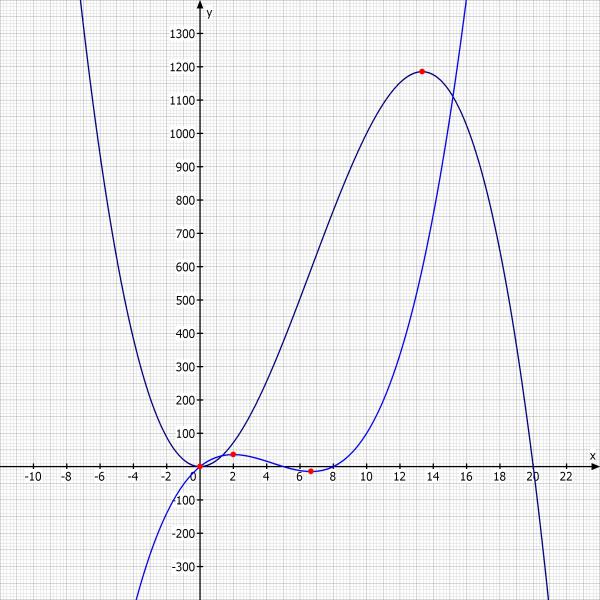
Skizze