f(x) = x^3 - 6x^2+ 9x; x ∈R
c) Bestimmen Sie den Punkt P (u | f(u) ) so, dass die Tangente an f(x) in P parallel zur Tangente an f(x) im Ursprung ist.
Steigung der Tangente im Ursprung? und in P?
f ' ( x) = 3 x^2 - 12x + 9
Im Ursprung: f ' (0) = 9
In P : f ' (u) = 3 u^2 - 12u + 9 | gleichsetzen =9
3 u^2 -12u + 9 = 9 |-9
3 u^2 - 12 u = 0
3u ( u- 4) =0
u1 = 0; schon bekannt (Ursprung) t1 : y = 9x + 0
u2 = 4; f(u2)= f(4) = 4^3 - 6*4^2 + 9*4 = 4 P(4/4)
t2 : y = 9x + q P einsetzen
4 = 9*4 + q
-32 = q
t2: y = 9x -32
Probe: Plott
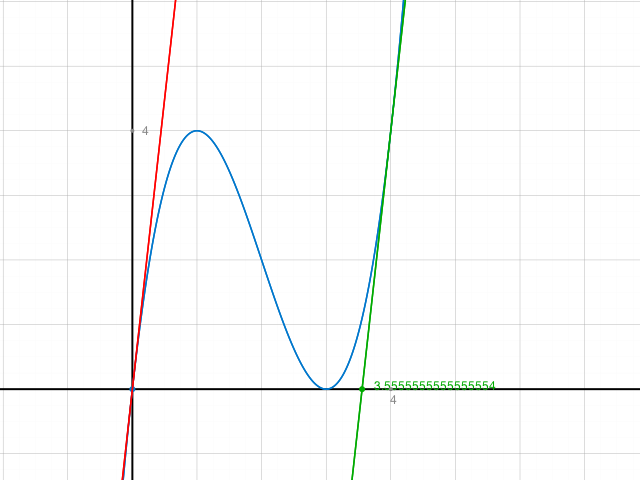
Die Nullstellen die Akelei schon berechnet hat bei der Faktorisierung sind hier ablesbar als 0 und 3
Deshalb f(x) = a x(x-3)2 a nicht direkt aus der Skizze ablesbar. Ist aber 1.