du kannst es auch anders machen. Hier mal mein Vorschlag dazu. Betrachte zunächst die Ebene von Oben. Jetzt wird die Ebene so gekippt, sodass Punkt F nach unten wandert und E nach oben. Was wirst du sehen? Richtig. Die von E zu S1 und S2 ausgehenden Seiten schließen in E einen immer größeren Winkel ein und die von F ausgehenden Seiten einen immer spitzeren Winkel. Man hat also einen Drachen als Grundfläche, da die Ebene an der Strecke S1S2 gedreht wird.
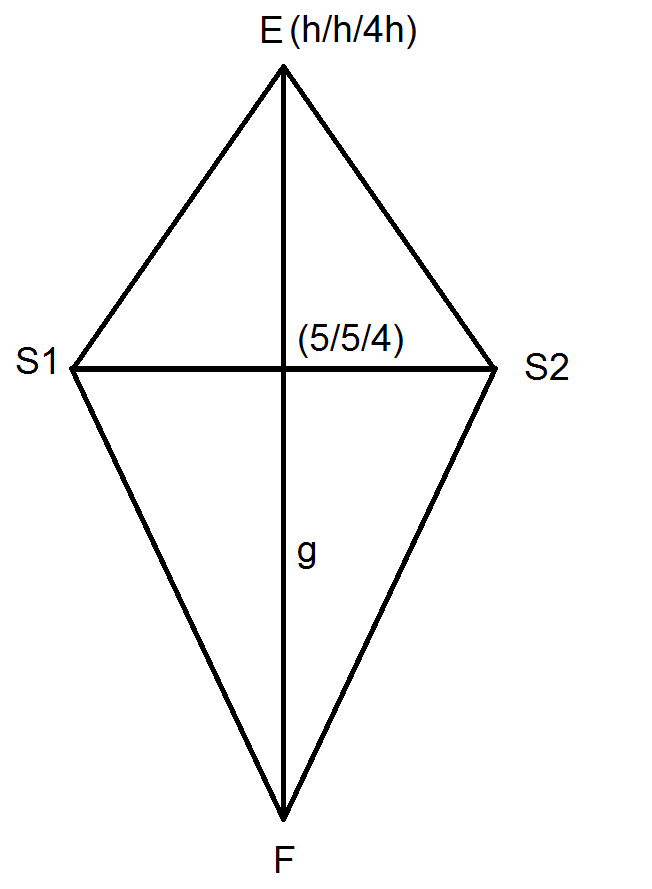
Nun kann man also eine Geradengleichung aufstellen, die durch den Mittelpunkt dieser Strecke geht und durch E. Sie lautet dann
$$ g:\vec{x}=\begin{pmatrix}h\\h\\4h\end{pmatrix}+w\cdot\begin{pmatrix}5-h\\5-h\\4-4h\end{pmatrix} $$
Diese Gerade wird auch in einem Punkt die Strecke schneiden, welche durch B und die von schräg oben betrachtet dem Betrachter am nächsten liegende Ecke, K(8/8/8) verläuft. Durch ihr verläuft folgende Gerade:
$$ k:\vec{x}=\begin{pmatrix}10\\10\\0\end{pmatrix}+t\cdot\begin{pmatrix}-2\\-2\\8\end{pmatrix} $$
Nun werden beide Geraden gleichgesetzt, um ihren gemeinsamen Schnittpunkt zu ermitteln:
$$ \begin{aligned}g&=h\\\begin{pmatrix}h\\h\\4h\end{pmatrix}+w\cdot\begin{pmatrix}5-h\\5-h\\4-4h\end{pmatrix}&=\begin{pmatrix}10\\10\\0\end{pmatrix}+t\cdot\begin{pmatrix}-2\\-2\\8\end{pmatrix} \\t\cdot\begin{pmatrix}2\\2\\-8\end{pmatrix}+w\cdot\begin{pmatrix}5-h\\5-h\\4-4h\end{pmatrix}&=\begin{pmatrix}10-h\\10-h\\-4h\end{pmatrix}\end{aligned} $$ Dann hat man folgendes LGS zu lösen. Habe dabei noch schonmal die dritte Zeile durch -4 geteilt.
$$ \begin{aligned}&1.)\quad 2t+(5-h)w&&=10-h \\&2.)\quad 2t+(5-h)w&&=10-h \quad |1.)-2.) \\&3.) \quad 2t+(-1+h)w&&=h \quad |1.)-3.) \end{aligned} $$
$$ \begin{aligned}&1.)\quad2t+(5-h)w&&=10-h \\&2.)\quad0&&=0 \\&3.)\quad (6-2h)w&&=10-2h \end{aligned}\\\Leftrightarrow w=\frac{h-5}{h-3} $$
w in 1.) ergibt dann :
$$ t=\frac{3h-5}{2h-6} $$
Jeweils in beide Geradengleichungen eingesetzt bekommt man:
$$ g:\vec{x}=\begin{pmatrix}h\\h\\4h\end{pmatrix}+\frac{h-5}{h-3}\cdot\begin{pmatrix}5-h\\5-h\\4-4h\end{pmatrix}=\frac{1}{h-3}\begin{pmatrix} 7h-25\\7h-25\\12h-20 \end{pmatrix} $$
$$ k:\vec{x}=\begin{pmatrix}10\\10\\0\end{pmatrix}+\frac{3h-5}{2h-6}\cdot\begin{pmatrix}-2\\-2\\8\end{pmatrix}=\frac{1}{h-3}\begin{pmatrix} 7h-25\\7h-25\\12h-20 \end{pmatrix} $$
Dieser Schnittpunkt entspricht dem Punkt
$$ F_h\Bigg(\frac{7h-25}{h-3}\Bigg|\frac{7h-25}{h-3}\Bigg|\frac{12h-20}{h-3}\Bigg) $$
Nun zu deiner Idee. Sie klappt auch. Du musst nur ein LGS lösen. Ansatz:
$$ E=g $$
$$ \begin{pmatrix}h\\h\\4h\end{pmatrix}+r\begin{pmatrix}9-h\\1-h\\4-4h\end{pmatrix}+s\begin{pmatrix}1-h\\9-h\\4-4h\end{pmatrix}=\begin{pmatrix}10\\10\\0\end{pmatrix}+t\begin{pmatrix}-2\\-2\\8\end{pmatrix} $$
$$ \Leftrightarrow\\t\begin{pmatrix}2\\2\\-8\end{pmatrix}+r\begin{pmatrix}9-h\\1-h\\4-4h\end{pmatrix}+s\begin{pmatrix}1-h\\9-h\\4-4h\end{pmatrix}=\begin{pmatrix}10-h\\10-h\\-4h\end{pmatrix} $$
$$\begin{aligned} &1.)\quad 2t+(9-h)r+(1-h)s&&=10-h\\&2.)\quad2t+(1-h)r+(9-h)s&&=10-h \\&3.)\quad-8t+(4-4h)r+(4-4h)s&&=-4h\quad |:(-4) \end{aligned}$$
$$\begin{aligned} &1.)\quad 2t+(9-h)r+(1-h)s&&=10-h\\&2.)\quad2t+(1-h)r+(9-h)s&&=10-h\quad| 1.)-2.) \\&3.)\quad2t+(-1+h)r+(-1+h)s&&=h\quad |1.)-3.) \end{aligned}$$
$$\begin{aligned} &1.)\quad 2t+(9-h)r+(1-h)s&&=10-h\\&2.)\quad0+8r+(-8)s&&=0\\&3.)\quad0+(10-2h)r+(2-2h)s&&=10-2h\quad |:2 \end{aligned}$$
$$\begin{aligned} &1.) \quad2t+(9-h)r+(1-h)s&&=10-h\\&2.)\quad0+8r+(-8)s&&=0\\&3.)\quad0+(5-h)r+(1-h)s&&=5-h\quad |(5-h)\cdot 2.)-8\cdot3.) \end{aligned}$$
$$\begin{aligned} &1.) \quad2t+(9-h)r+(1-h)s&&=10-h\\&2.)\quad0+8r+(-8)s&&=0\\&3.)\quad0+0r+(-48+16h)s&&=-40+8h\quad|:(-48+16h)) \end{aligned}\\s=\frac{h-5}{2h-6}\stackrel{2.)}{=}r\\ t=\frac{5-7h}{2h-6}$$
Durch Probeeinsetzung sieht man, dass eine wahre Aussage erzielt wird.
$$ \begin{pmatrix}h\\h\\4h\end{pmatrix}+\frac{h-5}{2h-6}\begin{pmatrix}9-h\\1-h\\4-4h\end{pmatrix}+\frac{h-5}{2h-6}\begin{pmatrix}1-h\\9-h\\4-4h\end{pmatrix}=\frac{1}{h-3}\begin{pmatrix} 7h-25\\7h-25\\12h-20 \end{pmatrix} $$
$$ \begin{pmatrix}10\\10\\0\end{pmatrix}+\frac{5-7h}{2h-6}\begin{pmatrix}-2\\-2\\8\end{pmatrix}=\frac{1}{h-3}\begin{pmatrix} 7h-25\\7h-25\\12h-20 \end{pmatrix} $$
Und man erhält auch hier wieder:
$$ F_h\Bigg(\frac{7h-25}{h-3}\Bigg|\frac{7h-25}{h-3}\Bigg|\frac{12h-20}{h-3}\Bigg) $$
Fertig.