Breite vom Fluss berechnen (sin,cos,tan)

Question

Von der Spitze eines Turms (h 28,6m), der e = 6m vom Ufer eines Flusses enfernt ist. erscheinen die beiden Flussufer unter dem Sehwinkel alpha = 17° Wie breit ist der Fluss? Fertige eine Skizze an.

Kann mir da bitte jemand helfen

Answer 1

Ich hoffe, dass ich das richtige deute:

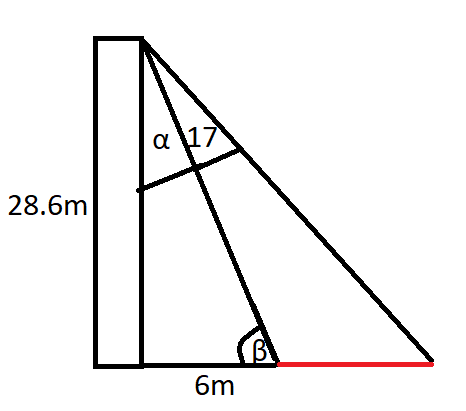
Wir können den WInkel rechts bei den 6m wie folgt berechnen:

tan(β)=28.6/6   |arctan(...)

β=arctan(28.6/6)

β=78.15°

Über die Winkelsumme können wir dann den Winkel oben links bestimmen:

α=180-90-78.15

α=11.85°

Der gesamte Winkel oben ist also

17+11.85=28.85°

Die gesamte Strecke berechnen wir wie folgt:

tan(28.85)=x/28.6  |*28.6

 x=9.764m

Das jetzt noch von den 6m abziehen

rote Linie=9.764m-6m

Rote Linie=3.764m

Answer 2

Sei x die Breite des Flusses, A die Spitze und C der Fußpunkt des  Turms

Dann berechnet sich BA mit Pyihagoras,α mit demTangens und der Komprementärwinkel zu α sei β. Dann hilft der Sinussatz.

Answer 3

gesucht ist α   tan α = 6 /28,6    | taschenrechener tan^-1

                                     α=  11,848°

                      x ist die gesuchte Breite

                      tan (α+17°)= (x+6)/28,6     |  *28,6

                            15,15   =x+6                | -6

                                 9,75= x

     A:           Der Fluß ist  9,75 m breit