Das kommt ein wenig darauf an, was du bereits weißt.
1. Möglichkeit:
Wenn du Ableitungen kennst, ...
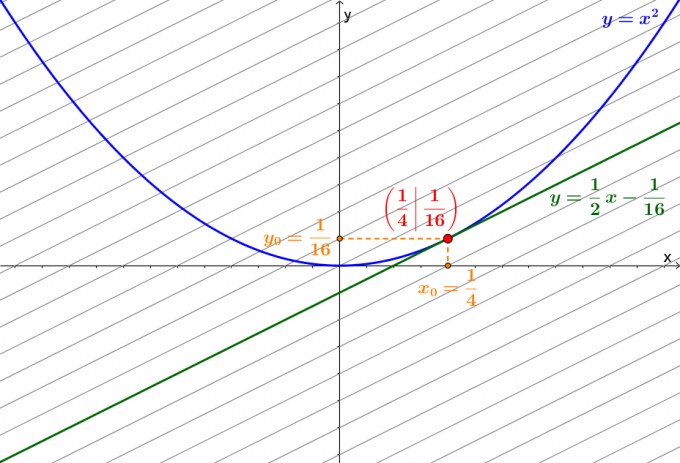
Die Geraden der Parallelenschar haben jeweils Steigung \(\frac{1}{2}\). Suche demnach die Stelle \(x_0\in\mathbb{R}\), an der die Tangentensteigung der Parabel gleich \(\frac{1}{2}\) ist. Die Parabel wird durch die Funktion \[f : \mathbb{R}\to\mathbb{R},\quad x\mapsto x^2\] beschrieben. Die Tangentensteigung der Funktion an der Stelle \(x_0\) ist der Wert \(f'(x_0)\) der Ableitung \(f'\).
Berechne demnach die Ableitung \(f'\) und löse die Gleichung \(f'(x_0) = \frac{1}{2}\), um die Stelle \(x_0\) zu erhalten. Damit hast du dann die \(x\)-Koordinate des Berührpunktes gefunden. Die \(y\)-Koordinate erhältst du dann durch \(y_0 = x_0^2\), da der Berührpunkt auf der Parabel liegt. Damit hast du dann den Berührpunkt \((x_0| y_0)\) berechnet.
[spoiler]
\(f(x) = x^2\)
\(f'(x) = 2x\)
Nun soll \(f'(x_0) = \frac{1}{2}\) sein. \(f'(x_0) = \frac{1}{2} \quad \Longleftrightarrow \quad 2 x_0 = \frac{1}{2} \quad \Longleftrightarrow \quad x_0 = \frac{1}{4}\)
Da der Berührpunkt \((x_0 | y_0)\) außerdem auf der Parabel liegt ... \(y_0 = x_0^2 = \left(\frac{1}{4}\right)^2 = \frac{1}{16}\)
Demnach ist \(\left(\frac{1}{4}\middle|\frac{1}{16}\right)\) der gesuchte Berührpunkt.
[/spoiler]
2. Möglichkeit:
Für welchen Parameter \(b\in\mathbb{R}\) gibt es nur einen Schnittpunkt? Also für welchen Parameter \(b\in\mathbb{R}\) hat die Gleichung \(x^2 = \frac{1}{2}x + b\) genau eine Lösung \(x\in\mathbb{R}\)?
Der entsprechende Schnittpunkt ist dann der gesuchte Berührpunkt.
[spoiler]
\(x^2 = \frac{1}{2}x + b \quad \Longleftrightarrow\quad x^2 - \frac{1}{2} x -b = 0\)
Wann wird die Diskriminante \(\left(\frac{1}{2}\right)^2 - 4\cdot 1\cdot (-b)\) der quadratischen Gleichung gleich \(0\)? \(\begin{aligned}\left(\frac{1}{2}\right)^2 - 4\cdot 1\cdot (-b) = 0 \quad & \Longleftrightarrow \quad \frac{1}{4} + 4 b = 0 \\ &\Longleftrightarrow \quad 4 b = -\frac{1}{4} \\ & \Longleftrightarrow \quad b = -\frac{1}{16}\end{aligned}\)
Berechne demnach den Schnittpunkt der durch \(y = x^2\) gegebenen Parabel mit der durch \(y = \frac{1}{2} x - \frac{1}{16}\) gegebenen Geraden.
\(\begin{aligned}x^2 = \frac{1}{2} x - \frac{1}{16} \quad & \Longleftrightarrow \quad x^2 - \frac{1}{2} x + \frac{1}{16} = 0 \\ & \Longleftrightarrow \quad x^2 - 2\cdot\frac{1}{4} x + \left(\frac{1}{4}\right)^2 = 0 \\ & \Longleftrightarrow \quad \left(x-\frac{1}{4}\right)^2 = 0 \\ & \Longleftrightarrow \quad x-\frac{1}{4} = 0 \\ & \Longleftrightarrow \quad x = \frac{1}{4}\end{aligned}\)
Demnach ist \(x_0 = \frac{1}{4}\) die \(x\)-Koordinate des Berührpunkts.
Da der Berührpunkt \((x_0 | y_0)\) außerdem auf der Parabel liegt ... \[y_0 = x_0^2 = \left(\frac{1}{4}\right)^2 = \frac{1}{16}\]
Demnach ist \(\left(\frac{1}{4}\middle|\frac{1}{16}\right)\) der gesuchte Berührpunkt.
[/spoiler]