du könntest es zum Beispiel so machen, wie es in der folgenden Skizze beschrieben wird.
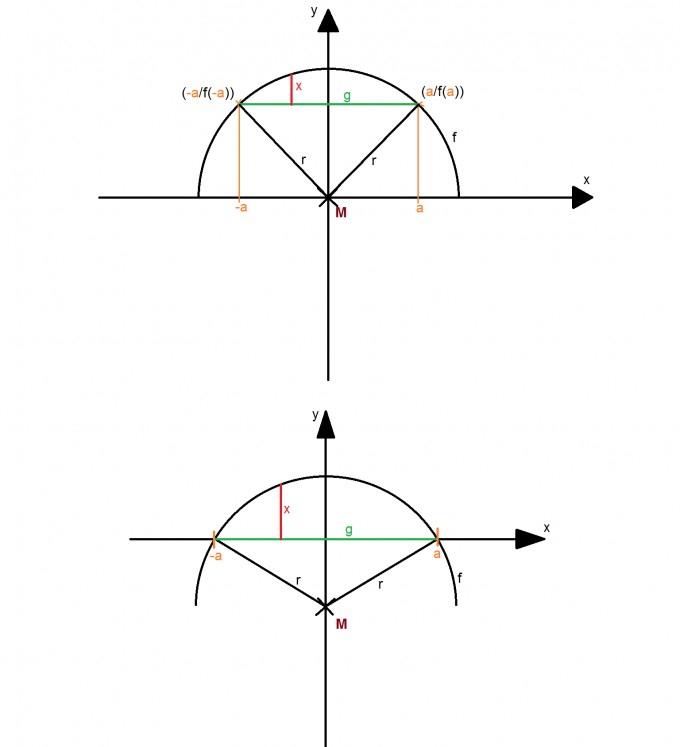
Man hat einen (Halb-)Kreis mit dem Radius r. Diese wird durch die Funktion $$ f(x)=\sqrt{r^2-x^2} $$ beschrieben. Nun wird eine Sehne in Form einer Geraden g so konstruiert, so dass ihre Endpunkte genau auf der Kreislinie liegen und parallel zur x-Achse verläuft. Die Gerade lässt sich durch f an einer belibiegen Stelle a beschreiben. $$ g(x)=f(a),\quad -a\leq x\leq a $$
Nun verschiebt man den Kreisbogen solange, so dass g in der x-Achse liegt, so dass man eine neue Funktion vom Halbkreis erhält $$ h(x):=f(x)-f(a)=\sqrt{r^2-x^2}-\sqrt{r^2-a^2},\quad -a\leq x\leq a $$
Somit gibt h auch den Abstand eines belibiegen Punktes auf der Sehne zur Kreislinie an, so dass sich die rote Strecke wie folgt berechnen lässt:
$$ X:=f(x)-f(a)=\sqrt{r^2-x^2}-\sqrt{r^2-a^2},\quad -a\leq x\leq a $$