allgemeine Lösung von Differentialgleichungen

Question

ich habe Differentialgleichungen y'x = y + sqrt(x^2+y^2)

Bis jetzt habe ich die Differentialgleichungen immer so gelöst das ich nach y' aufgelöst habe und dann y' = dy / dx geschrieben habe und alles was mit y zu tun hatte auf die dy Seite gebracht und alles was mit x zu tun hatte auf die dx Seite. Und dann von beiden das Integral ausgerechnet und danach wieder nach y aufgelöst damit ich die Lösung erhalte.

Die Lösung kommt durch Substitution von u = y/x auf die Lösung.

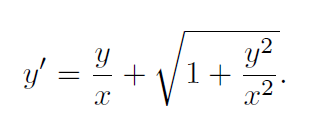
Aber wenn ich für y/x substituiere kommt bei mir heraus:

u = y/x

u' = -y / x^2 -> dx = (du / -y) * x^2

Und dann habe ich Integral von u + sqrt(1 u^2) 1/-y * x^2 du

Aber so komme ich nicht auf die Lösung.

Es wäre nett wenn mir jemand weiter helfen könnte. :)

Answer 1

Hallo

deine Ableitung ist falsch.

u=y/x -> u'=y'/x-y/x^2 und damit y'=u'*x+u

das jetzt in die umgeformte Dgl einsetzen und du hast due Dgl für u.

u'*x+u=u+√(1+u^2)

oder u'/√(1+u^2)=1/x

kommst du jetzt zur Lösung?

Gruß lul

Answer 2

Falls Du diese DGL meinst :

y' =y/x +sqrt(1 +y^2/x^2)

z=y/x

y=z*x

y'= z+z' x

->eingesetzt in die DGL:

z+z' x = z +√ (1 +z^2) |-z

z' x = √ (1 +z^2)

dz/dx *x= √ (1 +z^2)

dz/(√(1+z^2) = dx/x

arc sinh(z)= ln|x|+C

z= sinh(ln|x| +C)

Resubstitution: z=y/x

y/x=sinh(ln|x| +C)

y= x *sinh(ln|x| +C)