guten Abend!
Ich komme seit ein paar Stunden bei einer Aufgabe nicht weiter und hoffe, dass ihr mir helfen könnt.
Ich bearbeite gerade folgende Aufgabe:
Bestimmen Sie das Bild von f und entscheiden Sie, ob f injektiv ist.
Falls die Umkehrfunktion auf dem Bild von f existiert: ist sie stetig?
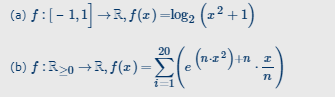
Ich habe meinen Ansatz in einem anderen Forum gepostet, aber da antwortet bis jetzt niemand und ich schreibe am Montag eine Klausur...
Deswegen seid mir nicht böse, wenn ich meine Lösungsansätze in Bildern schicke... Ich kann mit dem Formeleditor hier nicht so gut umgehen.
Meine Frage ist nun: Wie soll ich das Bild von solchen Funktionen bestimmen?
Mein Ansatz für die a) ist nämlich so:

Ich bin ein bisschen verwirrt, weil es ja sonst zu einfach wäre. Habe ich irgendwas übersehen oder mache ich das komplett falsch?
zu b)
Da habe ich leider keine Ahnung... Die Summe irritiert mich die ganze Zeit und weiß nicht, wie ich sie bei der Bestimmung des Bildes miteinbeziehen muss...
Aber da habe ich mir folgendes überlegt:
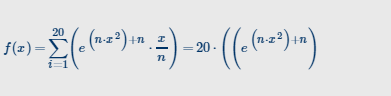
Kann man da so überhaupt schreiben?
Ich würde mich über euren Feedback und eurer Hilfe sehr freuen!
Mfg
Domenik