ich unterstelle, dass die Orte Bugbachau und Seewalchen beide gegenüber am See liegen. Und die Aufgabe besteht darin, die Entfernung dieser beiden Orte in Abhängigkeit der gegebenen Parameter zu berechnen. Zunächst brauchst Du dazu eine geometrische Vorstellung. Ich habe mal eine (nicht massstabsgetreue(!)) Prinzipskizze im Geoknecht3D eingegeben.
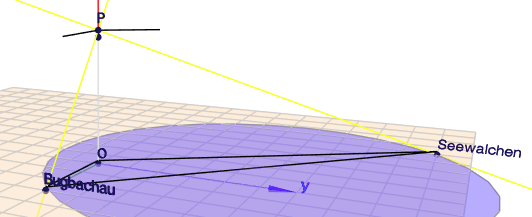
(klick auf das Bild und rotiere die Szene mit der Maus)
Dort siehst Du den See (blau) und die Lage der beiden Orte am See. Den Beobachtungspunkt habe ich mit \(P\) bezeichnet. Die Tiefenwinkel sind die Winkel, die von den schwarzen Strecken ausgehend von \(P\) nach unten zu den gelben Beobachtungsgeraden führen. Der Punkt unterhalb von \(P\) gibt die Höhe des Schoberstein an. Der Beobachter selbst steht darauf und sein Winkelmesser befindet sich nochmal 1,5m über diesem Standort. Das bedeutet, dass die relative Höhe von \(P\) oberhalb der Orte $$|OP| = 566 \text{m} + 1,5 \text{m} = 567,5 \text{m}$$ beträgt . Mit dieser Information und aus den beiden rechtwinkligen Dreiecken \(\triangle OBP\) und \(\triangle OSP\) kann man nun die beiden Strecken \(|OB|\) und \(|OS|\) berechnen (\(B\) = Bugbachau; \(S\) = Seewalchen).
$$\tan \alpha = \frac{|OP|}{|OB|} \space \Rightarrow |OB|= \frac{|OP|}{\tan \alpha} = \frac{567,5 \text{m}}{\tan 7,25°} = 4461 \text{m}$$
$$\tan \beta = \frac{|OP|}{|OS|} \space \Rightarrow |OS|= \frac{|OP|}{\tan \beta} = \frac{567,5 \text{m}}{\tan 1,93°} = 16841 \text{m}$$
Aus dem Cosinussatz im Dreieck \(\triangle OBS\) folgt nun die Strecke \(BS\); als Mass für die Länge des Sees:
$$|BS| = \sqrt{ |OB|^2 + |OS|^2 -2 \cdot |OB|\cdot |OS| \cdot \cos(\gamma) } \approx 19,36 \text{km}$$