Sigma Regeln (Erwartungswert+Standardabweichung)

Question

Bestimmen sie den Erwartungswert und die Standardabweichung der Binomialverteilung sowie die Wahrscheinlichkeit des

σ-Intervalls. Skizzieren Sie den Graphen. Vergleichen Sie mit dem Nährungswert für die σ-Umgebung. p=0,5 n=10

Brauche Hilfe

Answer 1

Erwartungswert:

μ=10*0.5=5

Standardabweichung:

σ=√(10*0.5*(1-0.5))=0.5√10

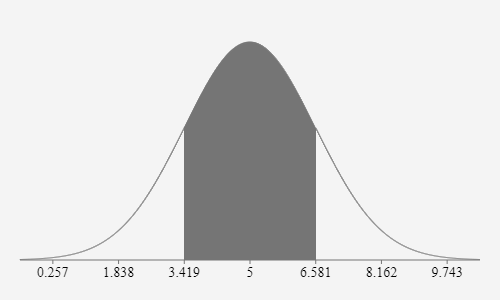
Wahrscheinlichkeit der einfachen Sigma-Umgebung:

P(μ-σ≤X≤μ+σ) wird gesucht, das heißt:

P(5-0.5√10 ≤ X ≤ 5+0.5√10)≈P(3.42≤X≤6.58)

Das kannst du nun einfach ganz normal berechnen:

P(3.42≤X≤6.58)=Φ((6.58-5)/(0.5√10)-Φ((3.42-5)/0.5√10)

P(3.42≤X≤6.58)=Φ(0.999)-Φ(-0.999)

P(3.42≤X≤6.58)=Φ(0.999)-(1-Φ(0.999))

Werte in der Tabelle ablesen. Ich erhalte:

P(3.42≤X≤6.58)=0.83891-(1-0.83891)

P(3.42≤X≤6.58)=0.67782

Comments

Beim Skizzieren fällt mir nun, dass du die Formel für die Gaußsche Glockenkurve nimmst. Dort Punkte einsetzt; diese in ein Koordiantensystem einzeichnest.