Warum muss ich hierfür die Formel umdrehen? Kann mir das einer bitte erklären?
Das sind die Fragen, die ich liebe, weil sie meines Erachtens zum Kern der Mathematik vordringen. Warum muss es \(D = E^{-1} \cdot A \cdot E\) heißen und nicht anders herum? (\(E\) sei die Matrix aus den Eigenvektoren). Ich möchte hier versuchen, dass ganz anschaulich zu erklären. Dazu wähle ich folgendes konkrete Beispiel. $$A= \begin{pmatrix} -1,4 & 1,2 \\ 1,2 & 0,4\end{pmatrix}$$ Damit fällt mir das Erklären leichter als mit dem \(A\) aus der Fragestellung. Das ändert aber am Prinzip rein gar nichts! Schauen wir uns zunächst an, was \(A\) tut, wenn ich die Abbildung, die (mein) \(A\) definiert, graphisch interpretiere.
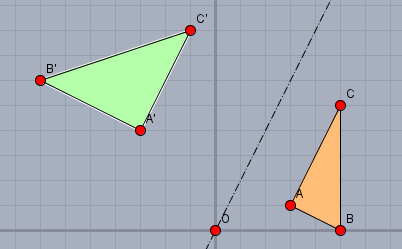
Dazu bilde ich das Dreieck \(\triangle ABC\) auf \(\triangle A'B'C'\) ab und sehe, dass es sich um eine Spiegelung inklusive einer Streckung senkrecht zur Spiegelachse handelt. Formal habe ich folgendes gemacht:
$$\triangle A'B'C' = A \cdot \triangle ABC = A \cdot \begin{pmatrix} 3 & 5 & 5 \\ 1 & 0 & 5 \end{pmatrix} = \begin{pmatrix} -3 & -7 & -1 \\ 4 & 6 & 8 \end{pmatrix}$$
Die Eigenwerte und Eigenvektoren von \(A\) sind $$\lambda_1 = -2; \quad \lambda_2 = 1; \\ e_1 = \begin{pmatrix} 2\\-1 \end{pmatrix}; \quad e_2 = \begin{pmatrix} 1\\2 \end{pmatrix}; \quad E=\begin{pmatrix} 2 & 1 \\ -1 & 2 \end{pmatrix}$$
Jetzt zeichne ich die Eigenvektoren in die Graphik ein:
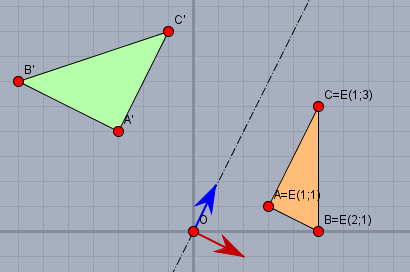
und nun ist es essentiell für das Verständnis, dass man sieht, was die Matrix \(E\) beschreibt. Dazu nenne ich das Koordinatensystem, in dem wir uns gerade tummeln, das 0-System. Die Eigenvektoren, die ja identisch mit den Spalten von \(E\) sind, sind im 0-System beschreiben (wo auch sonst!). Wenn ich nun einen der Punkte - z.B. \(^0C=\begin{pmatrix} 5 & 5 \end{pmatrix}^T\) mit den Eigenvektoren beschreibe, so steht dort: $$^0c= {^0e_1}\cdot r + {^0e_2} \cdot s = {^0e_1}\cdot 1 + {^0e_2} \cdot 3 \\ \space =E \cdot \begin{pmatrix} 1 \\ 3 \end{pmatrix}=\begin{pmatrix} 2 & 1\\1 & 2 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ 3 \end{pmatrix} = \begin{pmatrix} 5 \\ 5 \end{pmatrix}$$ Wähle ich also die Eigenvektoren als Basis, so hat der Punkt \(C\) dort die Koordinaten 1 und 3. \(E\) ist also so gesehen eine Transformation aus dem System der Eigenvektoren (das nenne ich das E-System) in das 0-System. Man kann man also jeden Punkt \(P\) damit vom 0-System in das E-System transformieren: $$^0p = E \cdot {^Ep}$$ die inverse Richtung gilt natürlich genauso $$^Ep = E^{-1} \cdot {^0p}$$ (probier's mal aus!).
Jetzt kommen wir zur Matrix \(D\). $$D = \begin{pmatrix} -2 & 0 \\ 0 & 1 \end{pmatrix}$$ und interpretieren \(D\) wieder als graphische Abbildung
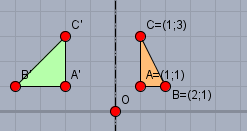
Ich habe oben das Dreieck \({^E \triangle ABC}\) mit \(D\) auf \({^E \triangle A'B'C'}\) abgebildet. Und dies ist doch die gleiche Abbildung, die \(A\) macht. Eine Spiegelung und eine Streckung um den Faktor 2 senkrecht zur Spiegelachse. Und die Koordinaten der Punkte sind alle aus dem E-System. Schließlich beschreibt \(D\) mit welchen Faktoren (die Eigenwerte) die Eigenvektoren bei der Abbildung mit \(A\) multipliziert werden. Es handelt sich hier also um das E-System. Möchte ich also einen Punkt \(P\) auf \(P'\) mit \(D\) abbilden, so müssen die Koordinaten von \(P\) im E-System angegeben werden. Rein formal heißt das:
$$^Ep' = D \cdot {^Ep}$$ wie kommt man aber zu \(D\) wenn man nur \(A\) hat? Nun dann transformiert man den \({^Ep}\) zunächst mal in das 0-Systen. Wie das geht, steht schon weiter oben $$^0p = E \cdot {^Ep}$$ anschließend wird die eigentliche Abbildung durchgeführt $$^0p' = A \cdot {^0p} = A \cdot E \cdot {^Ep}$$ gibt aber den Punkt im 0-System. D.h. der muss jetzt wieder in das E-System transformiert werden. Steht auch schon oben. Es ist: $$^Ep' = E^{-1} \cdot {^0p'} = \underbrace{E^{-1} \cdot A \cdot E}_{=D} \cdot {^Ep}$$ Ja - und deshalb heißt es $$D = E^{-1} \cdot A \cdot E$$ und umgekehrt gilt genauso $$A = E \cdot D \cdot E^{-1}$$ klar - oder?
Gruß Werner