Gleichseitiges Dreieck: Seiten mit Hilfe des Flächeninhaltes berechnen

Question

Aufgabe:

Ein gleichseitiges Dreieck hat einen Flächeninhalt A=15,3 cm². Berechne die Länge der Seiten.

Answer 1

Die Flächenformel für ein gleichseitiges Dreieck lautet:

$$ A = \frac { \sqrt { 3 } } { 4 } · a ^ { 2 } $$

Du kennst den Flächeninhalt A = 15,3 cm². Diesen kannst du in die Formel einsetzen und nach a auflösen:

$$ \begin{array}{l}{A=\frac{\sqrt{3}}{4} · a^{2}} \\ {15,3 \; \mathrm{cm}^{2}=\frac{\sqrt{3}}{4} · a^{2}} \\ {15,3 \; \mathrm{cm}^{2}=a^{2} · \frac{\sqrt{3}}{4} \quad | · \frac{4}{\sqrt{3}}} \\ {15,3 \; \mathrm{cm}^{2} · \frac{4}{\sqrt{3}}=a^{2}} \\ {a^{2}=15,3 · \frac{4}{\sqrt{3}} \; \mathrm{cm}^{2} \quad | \sqrt{ ~~~}} \\ {a=\pm \sqrt{15,3 · \frac{4}{\sqrt{3}} \; \mathrm{cm}^{2}}} \qquad | \text{ negatives Ergebnis weglassen} \\ {a \approx \sqrt{35,3338 \; \mathrm{cm}^{2}}} \\ {a \approx 5,944 \; \mathrm{cm}}\end{array} $$

Answer 2

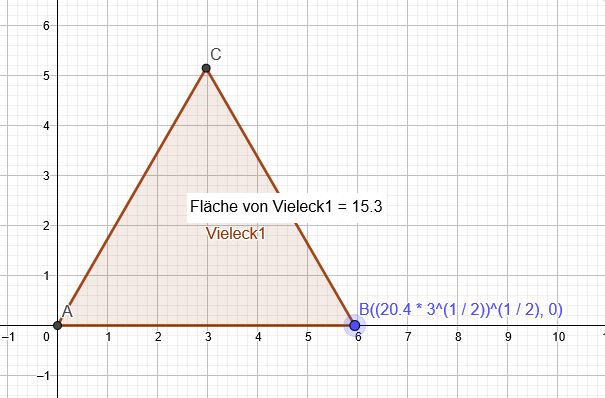
Ein gleichseitiges Dreieck hat einen Flächeninhalt \(A=15,3\) cm². Berechne die Länge der Seiten.

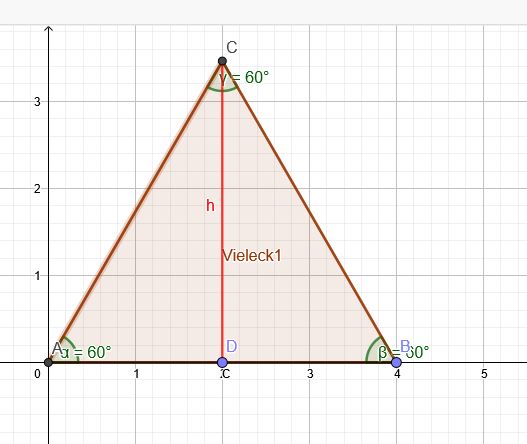
Fläche eines gleichseitigen Dreiecks:

\(15,3= \frac{c\cdot h}{2} \)

\(( \frac{c}{2})^2+h^2=c^2 \)

\(h^2=\frac{3}{4}c^2\)

\(h=\frac{c}{2}\sqrt{3}\)

\(15,3= \frac{c\cdot \frac{c}{2}\sqrt{3}}{2} =\frac{c^2}{4}\sqrt{3}\)

\(c^2=\frac{61,2}{\sqrt{3}}=\frac{61,2}{3}\sqrt{3}=20,4\sqrt{3}\)

\(c=\sqrt{20,4\sqrt{3}}≈5,94\)cm

a und b haben die gleiche Länge.