Schnittpunkt und Schnittwinkel von g und E bestimmen.

Question

hier ist die Aufgabe:

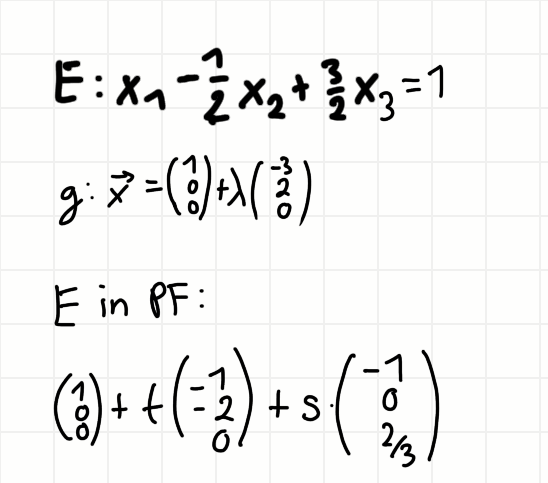
Als Schnittpunkt habe ich S(1,0,0)

Aber da ich ohne Rechner rechnen muss, habe ich gedacht, dass die beiden eventuell senkrecht sind.

Aber der Eigenvektor der Ebene und der Richtungsvektor der Geraden sind kein vielfaches von einander.

Identisch können die aber auch nicht sein, da ich nen Schnittpunkt bekomme...

Mfg

danke im Voraus

Comments

Als Schnittpunkt habe ich S(1,0,0)

Bis hierhin ist das richtig.

Answer 1

Aber der Eigenvektor der Ebene und der Richtungsvektor der Geraden sind kein vielfaches von einander.

Du meinst:

Aber der Normalenvektor der Ebene und der Richtungsvektor der Geraden sind kein Vielfaches voneinander.

Schau mal, was du als Argument von arcsin bekommst. Ein paar Sinuswerte und die zugehörigen Winkel kennst du bestimmt.

Die Parameterform der Ebenengleichung brauchst du nicht. Ausserdem ist sie unvollständig (keine Gleichung). S stimmt.

Comments

So viele Schreibfehler, sorry. Also ich habe Folgendes:

$$ \alpha = \operatorname { arccos } ( \frac { 4 } { \sqrt { 13 } \cdot \sqrt { \frac { 14 } { 4 } } } ] $$

und so würde ich das dann auch lassen, da ich keinen Taschenrechner verwenden darf und es kommt ja hier auch nichts bekanntes heraus.

---

Du kannst den Nenner auf

(√(13) * √(14)) /2  

bringen.

Dann ergibt sich im Argument von arcsin

8/(√(13*14)

Zeige mal deine Rechnung, falls du so ein Resultat nicht stehen lassen dürftest.

Verwende entweder arcsin oder rechne noch β = π/2 - α um den Schnittwinkel Gerade-Ebene β zu bekommen.

Das oben in der Annahme, dass du den Weg von hallo97 eingeschlagen hast. 

Answer 2

es geht einfacher.

Die Koeffizienten der Koordiantenform sind die Komponenten des normalen Vektors der Ebene E. Also berechnet sich dann ähnlich, wie bei zwei Vektoren, der Winkel wie folgt:

$$ \alpha=\arcsin\Bigg[\frac{\vec{n}\cdot \vec{r}}{|\vec{n}|\cdot |\vec{r}|}\Bigg] $$

$$ \vec{n}: Normalenvektor \ der \ Ebene\\ \vec{r}: Richtungsvektor $$