Es kommt halt auf den Kontext der Problemstellung an. So macht es in einigen Fällen durchaus Sinn 180° dazu zu addieren. Mal ein plumpes Beispiel. Du hast ein Dreieck
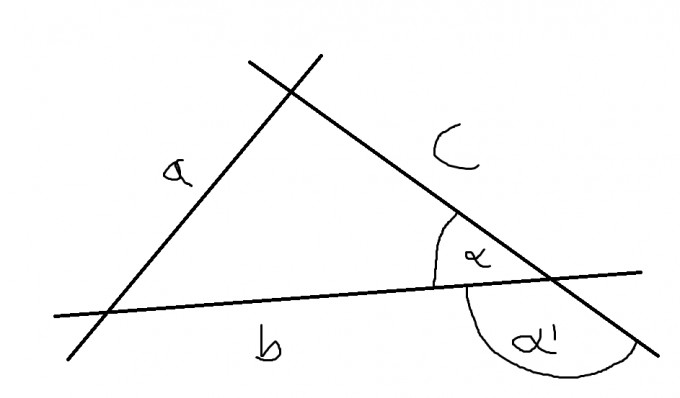
Nun sollst du - warum auch immer - den Winkel α' ausrechnen. Du hast aber zunächst α ausgerechnet. Nun bildest du die Differenz 180°-α=α' , womit du α' erhalten hast.
Oder du hast - wie im Link - einen Kreis. Dort ist der Winkel negativ. Du willst aber einen Winkel haben, der diesen Winkel als positive Zahl ausdrückt. Hier bildet man dann die Differenz
360°-β=β'.
Oder eine Turbinenschaufel steht so, dass sie mit einer Waagerechten einen negativen Winkel von -45° einschließt. Nun kommt etwas Wind, sodass sich die Turbine langsam gegen den Uhrzeigersinn dreht. Nach genau einer Umdrehung - was für ein Zufall - kommt sie zum stehen. Das Turbinenblatt hat eine 360°-Drehung gemacht.
Aber wie gesagt, wann man was wie dazuaddiert, hängt zu sehr vom Kontext ab. Ansonsten den Lehrer fragen, wie er sich das so vorstellt.