hier mal eine Skizze zu deiner Problemstellung.
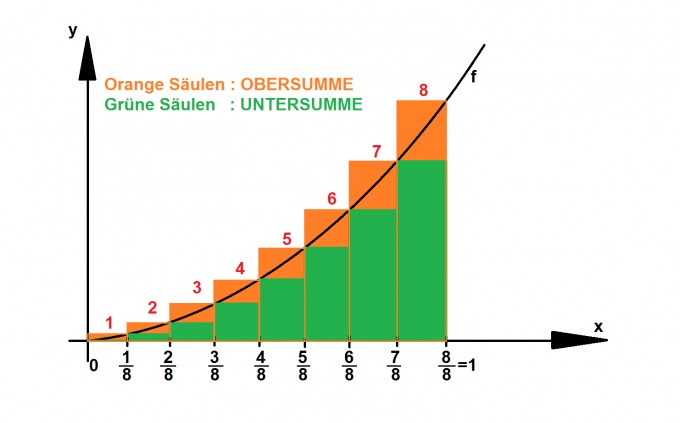
Im Bild siehst du, wie die Ober - und Untersumme ,,aussehen'' soll. Für die jeweilige Summe ist es nun wichtig, wo angefangen wird aufzusummieren. Bei der Obersumme geht es bei x=/8 los und endet bei x=1, bei der Untersumme geht man um eine Einheit nach links, sodass man bei x=0 anfängt und bei x=7/8 endet.
Der Flächeninhalt eines Rechtecks berechnet sich bekanntlich mit $$ A=l\cdot b $$. Die Breite ist hier b=1/8, da du eine Einteilung von 8 Rechtecken hast und die Länge (hier Höhe) wird durch x^2 beschrieben, also $$ l=f\Big(\frac{k}{8}\Big) $$
k ist einfach ein Laufindex, der jeweils die k-te Säule anspricht. Somit berechnet sich der Flächeninhalt des k-ten Rechtecks so: $$ A_k=\frac{1}{8}\cdot f\Big(\frac{k}{8}\Big) $$
Man hat $$ f(x)=x^2 $$
OBERSUMME
$$ O_8=A_1+A_2+...+A_7+A_8\\=\frac{1}{8}\cdot f\Big(\frac{1}{8}\Big)+\frac{1}{8}\cdot f\Big(\frac{2}{8}\Big)+...+\frac{1}{8}\cdot f\Big(\frac{7}{8}\Big)+\frac{1}{8}\cdot f\Big(\frac{8}{8}\Big)\\=\frac{1}{8}\cdot \Bigg(f\Big(\frac{1}{8}\Big)+f\Big(\frac{2}{8}\Big)+...+f\Big(\frac{7}{8}\Big)+f\Big(\frac{8}{8}\Big)\Bigg)\\=\frac{1}{8}\cdot \Bigg(\frac{1^2}{8^2}+\frac{2^2}{8^2}+...+\frac{7^2}{8^2}+\frac{8^2}{8^2}\Bigg)\\=\frac{1}{8}\cdot \frac{1}{8^2}\cdot (1^2+2^2+...+7^2+8^2)\\=\frac{1}{8^3}\cdot (1^2+2^2+...+7^2+8^2) $$
Für die Summe der Quadratzahlen gibt es eine Summenformel. $$ 1^2+2^2+3^2+...+n^2=\frac{n\cdot (n+1)\cdot (2n+1)}{6} $$ Hier wäre n=8, da wir in 8 Teile unterteilt haben. Also hat man
$$ O_8=\frac{1}{8^3}\cdot \frac{8\cdot (8+1)\cdot (2\cdot 8+1)}{6}=\frac{51}{128}=0,3984375 $$
Oder du rechnest die einfach per Hand zusammen, was bei so einer groben Einteilung noch geht. Anders wird es dann, wenn man eine viel feinere Einteilung, z.B., n=100 oder n=1000000 wählt. Da würde ein stumpfes Zusammenaddieren von Quadratzahlen ,,ein bisschen'' länger dauern und erst recht, wenn man den Fall n gegen ∞ betrachtet, um die exakte Fläche in diesem Intervall zu erhalten.
Die Untersumme überlasse ich dir. Bei Fragen/Unklarheiten melden.