Streifenmethode Archimeds Mathe

Question

Hallo , ich habe diese Aufgaben bekommen , aber ich weiß es nicht wie ich sie lösen soll

Die Aufgaben lauten :

a) f(x)=x+1,  I =[0;1]

b) f(x)=2-x,   I=[0;2]

c) f(x)=1/2x² , I =[0;1]

d) f(x)= x², I =[1;2]

e) f(x)=2x² + 1, I=[0;2]

f) f(x)= x⁴ , I=[0;2]

Mit Erklärungen bitte , also was in jeder Schritt gemacht wird .

Answer 1

Hallo,

die Funktion wird gezeichnet, dann die Fläche im angegebenem Intervall ermitttelt.mit der x Achse als "Grenze"

siehe auch hier : https://www.mathelounge.de/650721/unter-und-obersummen-einfuhrung-in-die-integralrechnung

Answer 2

Hallo,

mit der Steifenmethode werden Flächeninhalte annähernd bestimmt.

Bei a) wäre das diese Fläche

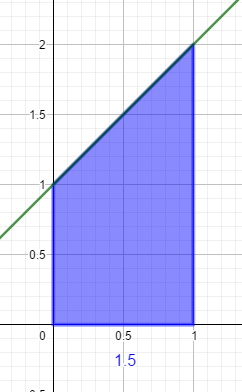
Es handelt sich um ein Trapez, dessen Flächeninhalt man leicht mit der entsprechenden Formel berechnen kann.

Würdest du die Fläche in 4 Rechtecke mit der Breite 0,25 einteilen, ergäbe die Summe ihrer Flächeninhalt 1,38

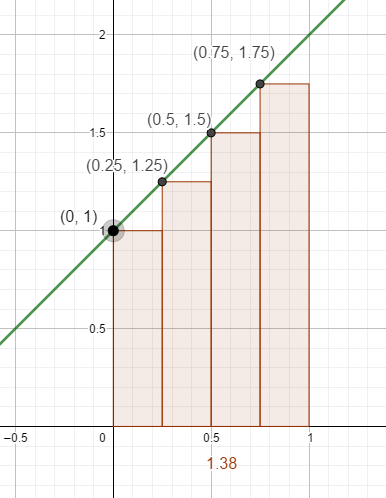
\(A=0,25\cdot 1+0,25\cdot 1,25+0,25\cdot 1,5+0,5\cdot1,75 = 1,375\)

Das Ergebnis wird genauer, je mehr Streifen du verwendest

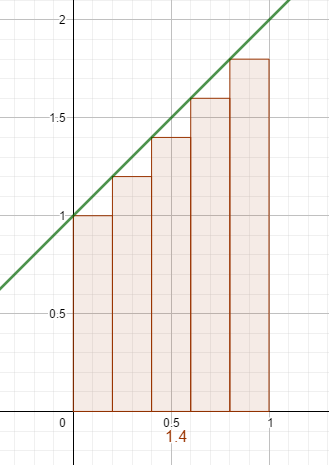
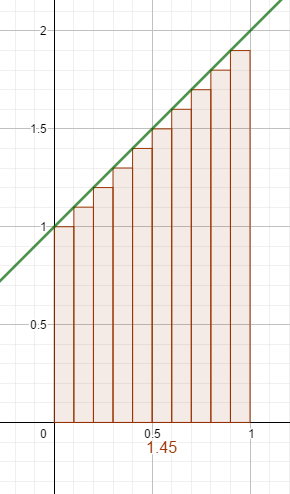
Gruß, Silvia