Bestimmen Sie die Gleichung der Geraden h, die durch den Punkt R= (-1, 4) verläuft und senkrecht auf der Geraden g, die durch die Punkte P= (-1, -1) und Q= (3, 1) verläuft steht.
Zeichnen Sie auch eine Skizze, in der g, h und die Punkte P, Q, R sowie dier Schnittpunkt S von g und h deutlich erkennbar ist.
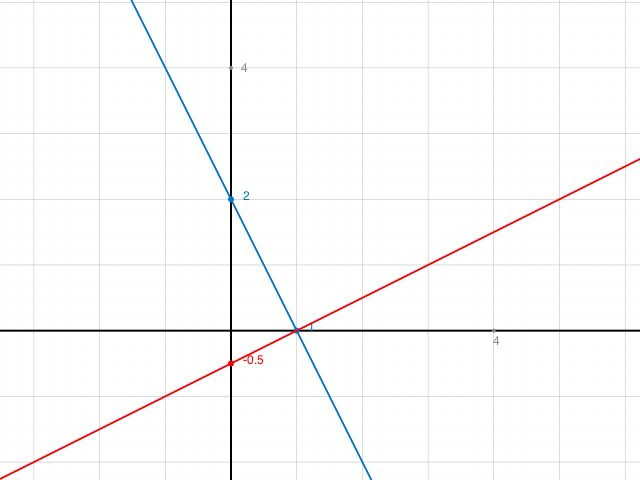
Gemäss https://www.mathelounge.de/56457/bestimmen-sie-die-gleichung-der-geraden-durch-die-punkte-und hat g die Gleichung g: y = 1/2 x - 1/2
Kontrolle der Gleichung von g:
-1 = 1/2*(-1) - 1/2 = -1 ok.
1 = 1/2*3 - 1/2 = 1 ok.
Lot auf g ist h:
hat die Steigung - 1/(1/2) = -2
Ansatz für h: y = -2x + q
R einsetzen: 4 = -2*(-1) + q = 2+q -----> q = 2
h: y = -2x + 2
Skizze, auf der du die Punkte einzeichnen kannst.
S(1|0) kann man berechnen.
-2x + 2 = 1/2x - 1/2 |+2x, + 1/2
2.5 = 2.5x |: 2.5
1=x
Dazu y berechnen y = -2*1 + 2 = 0
Daher S(1/0)
Noch eine Korrektur deiner Schreibweise. Bei Punkten sollte kein Gleichheitszeichen stehen:
Also nicht:
R= (-1, 4) verläuft und senkrecht auf der Geraden g, die durch die Punkte P= (-1, -1) und Q= (3, 1) verläuft steht.
Sondern:
R(-1, 4) verläuft und senkrecht auf der Geraden g, die durch die Punkte P(-1, -1) und Q(3, 1) verläuft steht.