Wie -> das hängt vom vorausgesetzten Wissensstand ab:
a) vor über 600 Jahren, als man noch nicht ableiten konnte:
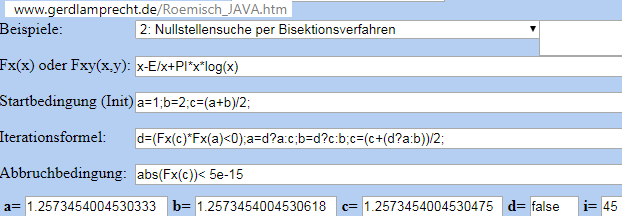
Bisektion (lese bei Wikipedia -> eine Art Probieren durch Bereichshalbierung) -> ergibt mit dem Iterationsrechner:
http://www.gerdlamprecht.de/Roemisch_JAVA.htm nach 45 Schritten etwa 14 richtige Nachkommastellen:
Zunächst allgemein mit e und Pi statt 4 und 2:
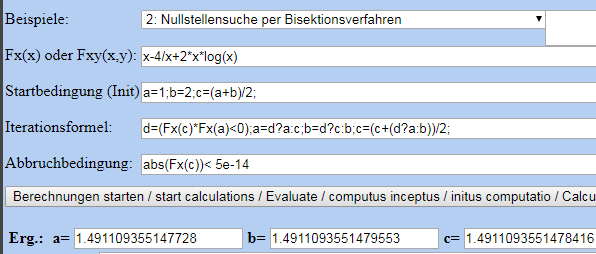
Bei Dir ist E nun 4 und Pi ist 2, was leichte Änderung ergibt:
b) kurz vor dem Jahre 1700 gabs https://de.wikipedia.org/wiki/Newton-Verfahren , welches mit Ableitung funktioniert:
http://www.gerdlamprecht.de/Roemisch_JAVA.htm#x-E/x+PI*x*log(x)@Na=0;@B0]=1;//Startwert@Nb=@Bi];a=@Bi+1]=b-Fx(b)/@Lb);@N@Aa-b)%3C4e-12@N1@N0@Nc=@Q29);
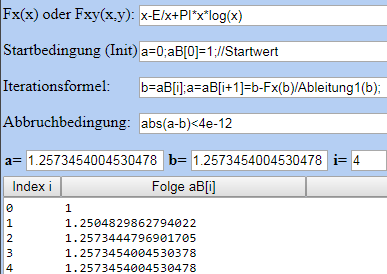
hier sind nur 4 Schritte nötig. (LINK beinhaltet bereits alle Parameter)
Bei Dir ist E nun 4 und Pi ist 2, was
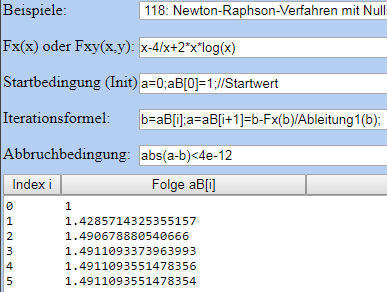 ergibt.
ergibt.
c) Heute ist die elementare Funktion LambertW(n,x) als Umkehrfunktion von x*e^x bekannt:
http://www.lamprechts.de/gerd/LambertW-Beispiele.html
x[n] = e^{1/2*LambertW(n,(2 e^{1 + 2/Pi})/Pi) - 1/Pi} ,n=-1...1 {also 3 Lösungen}
n | x[n]
----------
-1| -0.4147267156494321526805350203325 - 0.4473881564589946659329556046.. i
0 | 1.2573454004530476685095713076836...
1 | -0.4147267156494321526805350203325 + 0.4473881564589946659329556046.. i
Probe mit x-e/x+Pi*x*ln(x) ergibt für alle 3 x das richtige Ergebnis 0.
E nun 4 und Pi ist 2 ergibt
e^{1/2 W((2 e^{2/2}*4)/2) - 1/2}
=e^{1/2 W(4 e) - 1/2}
=e^{1/2 (W(4 e) - 1)}
x[n] = e^{1/2*(LambertW(n,4*e)-1)},n=-1...1 als Wertetabelle:
n | x[n]
-1| -0.6855221394300707493671270485448 - 0.58338247385457428273002381 i
0 | 1.491109355147835471047182943610787
1 | -0.6855221394300707493671270485448 + 0.58338247385457428273002381 i
ergibt x-4/x+2*x*log(x) für alle 3 x das richtige Ergebnis 0.
Wenn Du mehr Nachkommastellen benötigst, melde Dich (1000 Stück sind kein Problem).
Im letzten LINK findet man unten einige Rechner, die die Funktion LambertW kennen.
Lehrer ignorieren diese Funktion, obwohl sie seit Jahren bekannt ist und bei
https://de.wikipedia.org/wiki/Elementare_Funktion
aufgelistet wird.