Zufällige Zahl generieren

Question

ich möchte gerne eine zufällige Zahl zwischen 1 und 32 generieren. Ich kann es tun, indem ich 32 mal die Münze werfe.

Andere Vorgehensweise: Es ist ein Würfel (1-6) gegeben. Ich kann meine Funktion wie folgt definieren:

1,1 → 1

1,2 → 2

1,3 → 3

...

6,2 → 32

Wenn 6,3, 6,4, 6,5 oder 6,6 dann Wiederholung.

Frage: Ist das Verfahren genau so "sicher" bzw. zufällig wie das Münze-Werfen? Auf den ersten Blick würde ich "ja" antworten. Auf der anderen Seite bin ich mir unsicher, ob die Fälle 6,3 und größer, die eigentlich nicht sein dürfen, die Zufälligkeit irgendwie beeinflussen.

MfG

Answer 1

Ich denke mal, das geht so auch.

Ganz nett wäre aber auch das Werfen von 5 unterscheidbaren Münzen

 und sagst z.B.  Wappen =0 und Zahl = 1 und rechnest dann

1*Ergebnis von Münze 1 +   2*Ergebnis von Münze 2  + 4 * Ergebnis von Münze 3

+ 8* Ergebnis von Münze 4  +   16 * Erg. von Münze 5

Dann bekommst du in der Summe Zahlen von 0 bis 31 und addierst dann

immer 1 und hast so ganz nette Zufallszahlen von 1 bis 32.

Answer 2

Das ist eine schöne Aufgabe für den Iterationsrechner:

http://www.gerdlamprecht.de/Roemisch_JAVA.htm#floor(random(%20)*5.99999999999999)+1@NaB=Array();aD=Array(0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0);@N@Bi]=floor(random(%20)*31.99999999999999)+1;while((@Ci]=(Fx(i)-1)*6+Fx(i))%3E32){@Ci]=@Ci];}aD[@Bi]-1]++;aD[@Ci]+31]++;@Ni%3E100000@N0@N1@N#

aB sind Zufallszahlen von 1...32 gleichverteilt.

Fx(...) erzeugt Zufallszahl von 1...6 wie beim Würfel und mit

Fx(i)-1)*6+Fx(i) wird der 1. Wurf (0...5)*6 gerechnet und in Spalte aC abgelegt. Alles größer 32 wird verworfen und neu gewürfelt.

Um sehr viele "Würfe" zu bekommen, werden 100000 Zyklen durchgerechnet und die Häufigkeit verglichen:

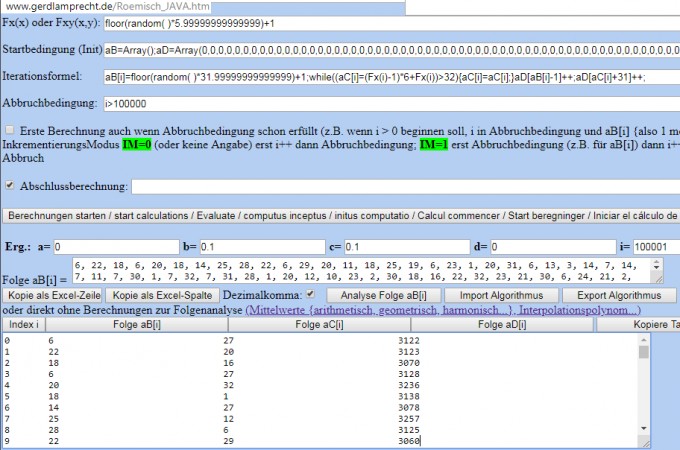
Jede Zahl (1...32) ist also etwa 100000/32=3125 mal vertreten.

Die Ergebnisse von aC (also den aus 2 6er Würfeln gebildeten Zahlen) werden in Spalte aD Index i=32...63 abgelegt.

Auf den 1. Blick sieht alles gleichverteilt aus.

Um noch mehr "Zufalls-Aussage" zu bekommen, habe ich das alles 9 mal wiederholt und die absolute Abweichung

der Spalte aC aufgelistet und in der letzten Spalte ALLES (also fast 1 Mio. Würfe) zusammengerechnet:

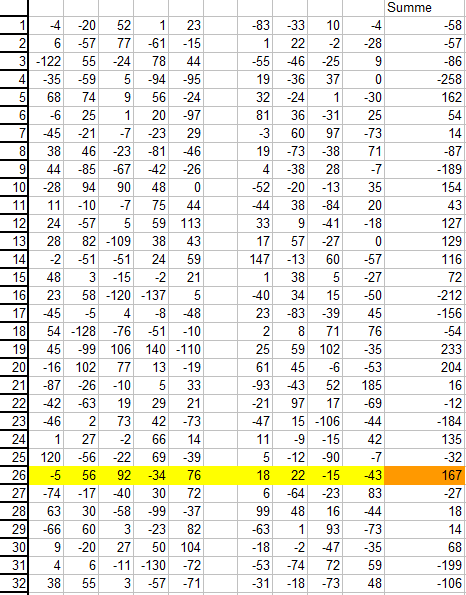
Nun sieht man beim Übergang von der 26 zur 27 einen minimalen Unterschied, weil die 26 immer sofort angenommen wird

(32-6=26 wird nie verworfen) und die hinteren ab 27 werden häufiger verworfen und neu gewürfelt. Das ist aber so minimal,

dass es schon kaum messbar ist! Die Funktion random() ist ja auch nur ein Pseudozufallsgenerator mit Periode um 10^600 herum. Für Eure Zwecke dürfte die Gleichverteilung daher ausreichen. (die 6 letzten verworfenen werden ja durch Neustart wieder neu aufgeteilt, was hier bis 10 Mio. in der Messgenauigkeit verschwindet).

Um noch bessere Aussagen zur Gleichverteilung zu bekommen müsste man Χ² Verteilungen und weitere Tests machen, die nicht mal die random-Funktion zu 100% (ideal Gleichverteilt) bestehen würde...