Suchen Sie Punkte zwischen A und C, für die die mittlere Steiggeschwindigkeit 16,07 ist.

Question

meine Frage bezieht sich auf den zweiten Teil einer Aufgabe. Im ersten Teil habe ich folgendes heraus gefunden:

Die mittlere Steiggeschwindigkeit zwischen A und C ist 16,07 m/min.

Die mittlere Sinkgeschwindigkeit zwischen E und G ist 11,54 m/min.

Nun der zweite Teil der Aufgabe:

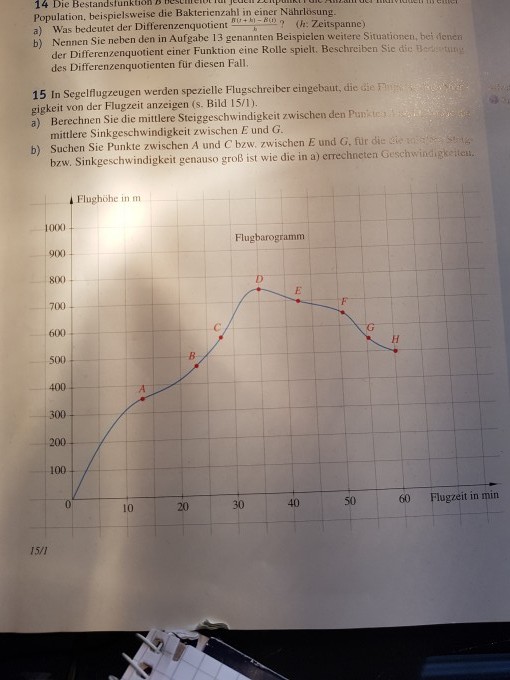
Suchen Sie Punkte zwischen A und C bzw. zwischen E und G, für die die mittlere Steig- bzw. Sinkgeschwindigkeit genauso groß ist wie die in a) errechneten Geschwindigkeiten.

Und dabei bin ich etwas überfordert. Mir ist klar, dass [f(b) - f(a) / b - a ] = 16,07 bzw. 11,54 sein muss. Aber weiter komme ich nicht. Die Punkte sind übrigens in einem KoSy eingezeichnet.

A(13|350) C(27|575) E(42|700) G(55|550)

Ich bedanke mich schonmal im Voraus für eure Hilfe.

Liebe Grüße

Answer 1

Zeichne einfach die Gerade durch A und B und verschiebe sie

parallel dass sie den Graphen in zwei anderen Punkten schneidet.

Für diese beiden hast du dann die gleiche mittlere

Geschwindigkeit.

Answer 2

Hallo

 du zeichnest die Gerade zwischen A und C, dann suchst du eine Parallele dazu, (zwischen A und C) die Tangente an die Kurve ist. dasselbe mit den anderen 2 Punkten, Da du nur einen Graphen hast geht das nätürlich nur nach gutem Augenmaß, ist also nicht exakt.

Gruß lul