Im Unterricht hatten wir das irgendwie so g x : (ein vektor) + t (zweiter vektor)
Das ist eine andere Art, eine Gerade zu beschreiben. Ich nutze mal deine Benennung.
(ein Vektor): Das ist der sogenannte Stützvektor (also ein Punkt!) einer Geraden.
(zweiter Vektor): Das ist der Richtungsvektor, der einfach die Differenz von dem Stützvektor und einem weiterem (Orts-) Vektor ist.
Ja, du liest richtig. Punkte können auch als Ortsvektoren angesehen werden.
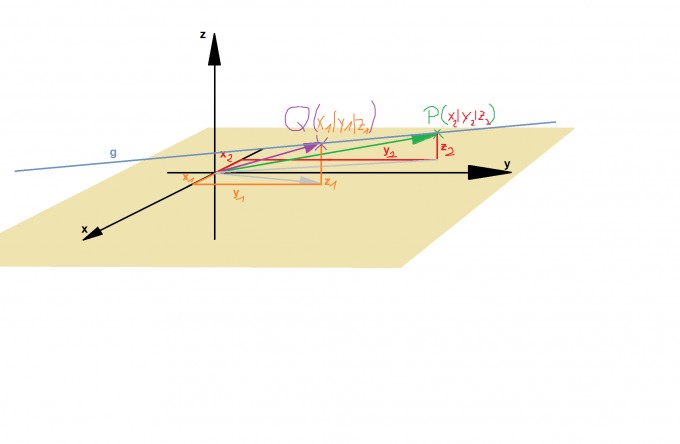
Punkt kann wiegesagt als ein Vektor beschrieben werden. Das wird dann so geschrieben:
$$ \vec{0q}=\begin{pmatrix} x_1\\y_1\\z_1 \end{pmatrix}, $$
für den Punkt Q(x_1|y_1|z_1) zum Beispiel. Und wenn du jetzt mal in die Skizze schaust, wirst du sehen, dass jede Zahl in einer Zeil, eine Verschiebung bedeutet. Und da wir im dreidimensionalen Unterwegs sind, sind es drei Verschiebungskomponenten (x-Richtung, y-Richtung, z-Richtung). Den Punkt P(x_2|y_2|z_2) kann man dann so beschreiben:
$$ \vec{0p}=\begin{pmatrix} x_2\\y_2\\z_2 \end{pmatrix} $$
Jetzt kann man mit zwei Punkten (Ortsvektoren) eine Gerade aufstellen. Lass uns Q als Stützvektor nehmen. Außerdem wollen wir, dass die Gerade durch P geht. Nun ist aber die Frage: Wie kommt man von Q nach P? Jetzt schaust du dir von beiden Punkten die einzelnen Komponenten an und bildest davon jeweils die Differenz. Dabei bekommst du einen neuen Vektor raus, den Richtungsvektor:
$$ \vec{r}=\begin{pmatrix} x_2-x_1\\y_2-y_1\\z_2-z_1 \end{pmatrix} $$
All diese Differenzen (sind auch wieder nur Zahlen) geben dir an, um wie viele Einheiten man sich komponentenweise bewegen muss, um von Q nach P zu gelangen.
Nun kann man sich auch überlegen, wie denn der Mittelpunkt von der Strecke P und Q lauten könnte. Und da ich von Mittelpunkt spreche, gehen wir nur jeweils komponentenweise die Hälfte, also multiplizieren unseren Richungsvektor r mit 0,5. Oder ich interessiere mich jetzt gerade für den Punkt der genau 1/4 des Abstandes beider Punkte P und Q von Q entfernt ist, d.h., man multipliziert den Richungsvektor r mit 0,25. Man könnte das jetzt ewig so weiter machen und bekäme unendlich viele Punkte, eine Menge von Punkten (Ortsvektoren), die sich durch eine Gerade beschreiben lassen.
$$ g:\vec{x}=\vec{0q}+t\cdot \vec{r} $$
Mit t kann man also jeden Punkt auf dieser Geraden erreichen, da man mit t einfach nur ein Vielfaches des Richungsvektors r nimmt und noch mit dem Stützvektor addiert.
Und diese neue Schreibweise, die du im Unterricht kennengelernt hast, lässt sich auch wieder auf die dir bereits vertraute Schreibweise zurückführen, nämlich y=m*x+n.