Ableitungsfunktion des Graphen f' einer Funktion f (einfache Aufgabe)

Question

Hallo liebe Mathegenies,

ich brauche ein wenig Hilfe bei der folgenden Aufgabe:

 

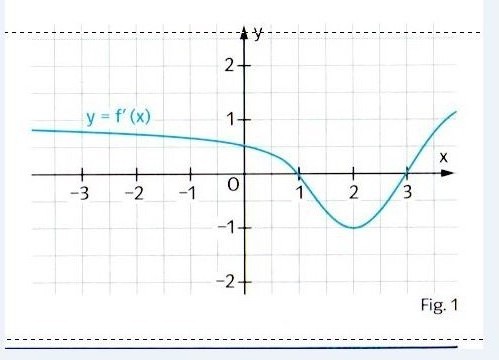
Das Foto zeigt den Graphen der Ableitungsfunktion f' einer Funktion f.

Welche der folgenden Aussagen sind wahr?

Begründe die Antwort in einfachen und verständlichen Worten

a) Die Funktion f ist im Intervall [0;2] streng monoton fallen.

b) Die Funktion f ist im Intervall [-2;0]  streng monoton wachsend.

c) Die Funktion f ist im Intervall [1;3] monoton fallend.

 

Ich würde mich sehr freuen, wenn Ihr mir dans ganze einfach erklärt(also eure Lösungen) und wieso es so ist.

 

:- )

Comments

Das ganze soll mit dem Monotoniesatz belegt werden.

Answer 1

Eine Funktion ist monoton steigend, wenn die Ableitung positiv ist. Sie ist fallend, wenn die Ableitung negativ ist.

a) falsch

b) richtig

c) richtig

Comments

Vielen Dank schonmal aber was meinst du hiermit genau:


Eine Funktion ist monoton steigend, wenn die Ableitung positiv ist. Sie ist fallend, wenn die Ableitung negativ ist.


Könntest du mir das vielleicht einmal für Doofe erklären :)

---

Angenommen, die Ableitung f' ist im Intervall [0, 3] größer als Null. Dann weiß man, dass die Funktion f in diesem Intervall monoton steigend ist.

---

Aber wieso ist sie größer als Null und ist -3;0 nicht auch positiv


Könntest du mir vielleicht den Ableitungsgraphen al Bild zuschicken ich werde auch einen machen und ihn hochladen mal sehen, wie er von deinem abweicht :)

---

So stelle ich es mir vor also f(x) ich weiß es leider nicht besser :(

---

Du hast ja eigentlich nur die Ableitungsfunktion etwas nach oben verschoben. So geht das nicht.

Man kann aus dem Graphen von f' einige Informationen ablesen: Da, wo f' eine Nullstelle hat, hat f ein Extremum. Da. wo f' ein Extremum hat, hat f einen Wendepunkt. Daraus kann man jetzt ungefähr den Graphen von f zeichnen. Natürlich kann man diesen beliebig nach oben oder unten verschieben, die Ableitung bleibt dabei die gleiche. Hier ist mein Versuch: