Hallo Lounger,
Du kannst Deine Ergebnisse - zumindest vom Augenschein her - prüfen, wenn Du die berechneten Größen im Geoknecht 3D eingibst. Ich habe das mal für Dich gemacht und man sieht, dass da offensichtlich was nicht stimmt:
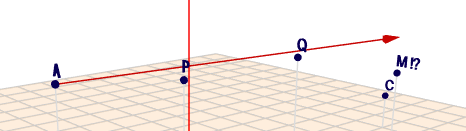
\(M\) liegt offensichtlich nicht zwischen \(B\) und \(C\), die Gerade geht nicht durch \(M\) und die Punkte \(A\), \(P\), \(Q\) und \(M\) liegen nicht auf einer Geraden (klick auf das Bild und rotiere die Szene mit der Maus).
Der Mittelpunkt \(M\) der Strecke \(BC\) ist $$M= \frac12(B+C) = \frac12 \left( \begin{pmatrix} -4\\4\\-5 \end{pmatrix} + \begin{pmatrix} -6\\2\\1 \end{pmatrix} \right) = \begin{pmatrix} -5\\3\\ \colorbox{#ffff00}{-2} \end{pmatrix}$$ Eine Gerade \(g\) durch \(A\) und \(M\) könnte so heißen: $$\begin{aligned} g: \space x &= A + r(M-A) \\&= \begin{pmatrix} 4\\0\\ 2,5 \end{pmatrix} + r \left( \begin{pmatrix} -5\\3\\ -2 \end{pmatrix} - \begin{pmatrix} 4\\0\\ 2,5 \end{pmatrix} \right) \\&= \begin{pmatrix} 4\\0\\ 2,5 \end{pmatrix} + r \begin{pmatrix} -9\\3\\ -4,5 \end{pmatrix} \end{aligned}$$ und die Drittelung der Strecke \(AM\) geht dann auch: $$P = A + \frac13(M-A) = \begin{pmatrix} 4\\0\\ 2,5 \end{pmatrix} + \frac13 \begin{pmatrix} -9\\3\\ -4,5 \end{pmatrix} \\ \space = \begin{pmatrix} 4\\0\\ 2,5 \end{pmatrix} + \begin{pmatrix} -3\\1\\ -1,5 \end{pmatrix} = \begin{pmatrix} 1\\1\\ 1 \end{pmatrix}$$ $$Q = A + \frac23(M-A) = \begin{pmatrix} 4\\0\\ 2,5 \end{pmatrix} + \frac23 \begin{pmatrix} -9\\3\\ -4,5 \end{pmatrix} \\ \space = \begin{pmatrix} 4\\0\\ 2,5 \end{pmatrix} + \begin{pmatrix} -6\\2\\ -3 \end{pmatrix} = \begin{pmatrix} -2\\2\\ -0,5 \end{pmatrix}$$ und augenscheinlich ist das wohl richtig.