Hallo
man sucht die Nullstelle einer Funktion f(x)
ich zeichne das für f(x)=1/3*x^2-2
es ist leicht eine Stelle zu finden, wo f(x)<0 ist ich nehme x=0, f(x)=-2 und eine wo f(x)>0 ist, ich nehme x=3, f(x)=1 jetzt bilde ich die Verbindungsgerade zwischen den 2 Punkten (0,-2) und (3,1)= also die Sekante y=x-2
davon bestimme ich die Nullstelle x=2
jetzt muss ich f(2) bestimmen f(2)=-2/3 also negativ, deshalb hab ich wieder einen negativen und einen positiven Punkt, wieder die Sekante zwischen (2,-2/3) und (3,1): y=1,65*x-3,95, wieder die Nullstelle bei x=2,39 f(2,39)=-0,09, negativ also wieder Sekante zu dem positiven Punkt, in der Zeichnung ist die funktion blau, die erste Sekante rot, die zweite grün, die dritte gelb, mit der dritten hat man x=2,44 erreicht und f(x)=-0,015 ist also nahe an 0.
da man den letzten Teil kaum mehr sehen kann hab ich ihn vergrößert ausgezeichnet-
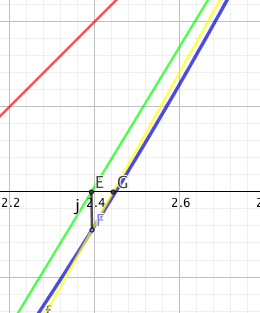
so macht man das mit jeder Funktion solange Sekanten bis f(x) nahe an 0 ist.