die 3x ergeben sich durch die durchschnittliche Wassermenge pro Sekunde. Wenn Du a) gelöst hast, weißt Du, dass insgesamt 360 Liter eingelaufen sind, diese durch 120 Sekunden geteilt ergibt 3.
Das Integral brauchst Du hier nicht unbedingt, da die Graphenabschnitte, um die es geht, linear sind, es ist also möglich, den Flächeninhalt unter dem Graphen, mit Hilfe der Formeln für rechtwinklige Dreiecke und Rechtecke zu berechnen.
Aber jetzt mal Schritt für Schritt:
a) Gefragt: Wasserstandshöhe nach 2 Minuten; Tabelle: eingelaufene Liter nach jeweils 10 Sekunden
Ich beginne mit dem offensichtlichen: Zeit 40-100 Sekunden
4l pro Sekunde für 60 Sekunden : 60*4=240 <- entspricht auch dem Quadrat der Einheiten oder dem Flächeninhalt unter dem Graphen
Nun der Beginn: Zeit 0-40 Sekunden
Wir haben 40 Sekunden und kommen bis zur 4l heran, dies sind die Katheten im rechtwinkligen Dreieck, daher gilt für den Flächeninhalt: $$ \frac{40*4}{2} $$ $$ \frac{40*2}{1} $$ oder 80l
Nun das Ende: Zeit 100-120 Sekunden
Wir haben 20 Sekunden und kommen von 4l bis 0l, wieder in die Katheten umgedacht: $$ \frac{20*4}{2} $$
$$ \frac{20*2}{1} $$ oder 40l
240+80+40=360
Es sind also insgesamt 360 Liter eingeflossen, ich Weiß, das steht soweit auch irgendwie auf deinem Zettel.
Es ist aber nach der Höhe gefragt, also noch schnell umgerechnet: 120cm*60cm*60cm=12dm*6dm*6dm
12*6*h=360 ; umformen nach h
$$h=\frac{360}{12*6}$$ $$h=\frac{30}{6}$$ $$h=\frac{5}{1}$$ oder 5, also beträgt die Füllhöhe 5dm oder 50cm.
Die Werte für die Tabelle
| Zeit | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 |
| Liter | 0 | 5 | 20 | 45 | 80 | 120 | 160 | 200 | 240 | 280 | 320 | 350 | 360 |
b) Naja, Graph dazu zeichnen der sieht in etwa so aus:
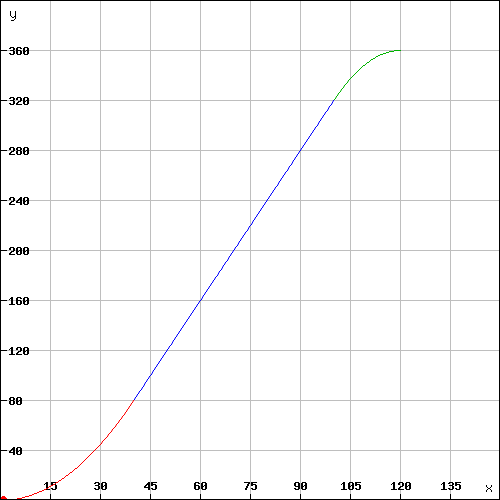
c: Nach meinem Verständis nach ist das mit den Teilabschnitten und den Funktionen so gemeint:
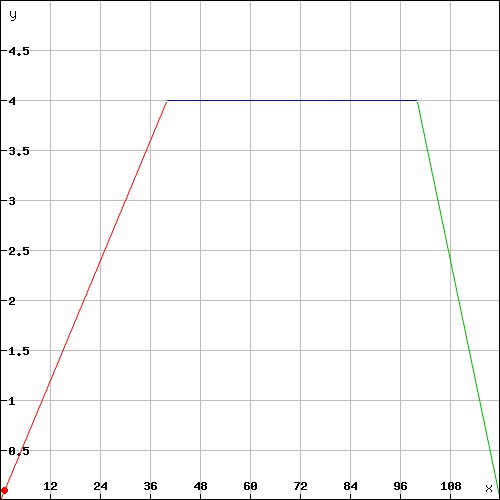
f1(x)=x/10 für 0≤x≤40
f2(x)=4 für 40≤x≤100
f3(x)=-(x/5)+24 für 100≤x≤120
( die +24; der Graph soll durch (100/4) gehen also setze ich ein
4=-(100/5)+b nach b umstellen
b=24)
und
W1(x) für 0≤x≤40 Kathete 1 : x; Kathete 2 : x/10
$$W_{1}(x)=x*\frac{x}{10}*\frac{1}{2}=\frac{x^2}{20}$$
W2(x) für 40≤x≤100 4l/pro Sekunde und die bereits vom anderen Graphen erfassten 80 Liter abziehen
W2(x)=4x-80
W3(x) für 100≤x≤120 Kathete 1 : x; Kathete 2 : -x/5
somit haben wir erstmal $$x*-\frac{1}{5}*x*\frac{1}{2}=-\frac{1}{10}x^2$$
Jetzt ist das hier mit dem Schnitt mit den anderen Achsen so eine Sache, einfach mal einen Wert abziehen und das passt, geht hier nicht. Wir wissen aber der Scheitelpunkt der Parabel ist (120/360), bei x=120 soll nämlich die Pumpe nichts mehr Pumpen und der Funktionswert soll 360 Liter annehmen. Die Scheitelform einer Parabel ist a(x-d)2+e, dabei ist in deinem Beispiel a=-1/10; d=120; e=360
also: $$W_{3}(x)=-\frac{1}{10}(x-120)^2+360$$
Wenn man will, kann man das auch noch ausklammern, zunächst binomische Formel anwenden
$$=-\frac{1}{10}(x^2-240x+14400)+360$$
ausmultiplizieren
$$=-\frac{1}{10}*x^2+24x-1440+360$$
zusammenfassen
$$=-\frac{1}{10}*x^2+24x-1080$$
Hoffe du kommst da jetzt besser durch, frag', wenn Du noch was brauchst.