Fläche und Umfang einer Herzfigur berechnen

Question

Wie berechne ich Fläche und Umfang davon?

Answer 1

Hallo Catwoman,

Die Skizze sollte wahrscheinlich so aussehen:

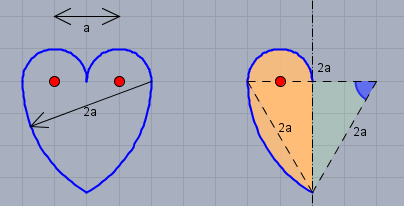
Da die Figur symmetrisch ist, reduziere ich das ganze auf die Hälfte und kommen zu der Figur rechts. Dort habe ich auch ein gleichseitiges Dreieck mit der Kantenlänge \(2a\) eingezeichnet. Daraus folgt dann der blaue Winkel mit \(60°\). Somit setzt sich der Umfang aus dem Halbkreis \(U_h\) und dem 6'tel Kreis \(U_6\) zusammen (360° : 60°=6):

$$U = 2(U_h + U_6) = 2(\colorbox{#ffff00}{π·a/2} + \frac16 \cdot 2\pi \cdot 2a) = \frac{7}{3}\pi a$$

Der Flächeninhalt der halben Figur ist das Tortenstück \(A_t\) minus dem angedeuteten Dreieck \(A_d\) rechts plus der Halbkreis \(A_h\) oben:

$$F = 2(A_t - A_d + A_h) = 2 \left(\frac16 \cdot \pi (2a)^2 - a^2 \cdot \frac12\sqrt{3} + \colorbox{#88ff88}{0.5π(0.5a) }\right) \\ \space = a^2\left( \frac43 \pi - \sqrt{3} + \frac14 \pi \right) = a^2 \left( \frac{19}{12} \pi - \sqrt{3} \right) \approx 3,24 a^2$$

Gruß Werner

PS.: zu den farblichen Markierungen siehe mein Kommentar unten

Comments

Warum istndas radius 2a und ich  verstehe das umfang des halbkreises nicht  und die fläche des halb kreis nicht

---

Hallo Catwoman,

Warum ist der Radius 2a ?

Betrachte folgende Skizze:

 

Der Abstand der Mittelpunkte der beiden Halbkreise ist mit \(a\) angegeben. Da die (Halb-)Kreise dicht an dicht liegen, muss ihr Radius \(r_h\) genau halb so groß sein. $$r_h = \frac a2$$ Der Radius des Kreisbogens \(r_t\) im unteren Teil ist so groß wie zwei Durchmesser - bzw. vier Radien - der Halbkreise. Macht: $$r_t = 4 r_h = 4 \cdot \frac a2 = 2a$$

.. verstehe den Umfang des Halbkreises nicht ...

Der Umfang \(U\) eines Kreises mit Radius \(r\) ist \(U=2\pi r\). Der Umfang \(U_h\) eines Halbkreises mit Radius \(r_h = a/2\) ist halb so groß: $$U_h = \frac12 U = \frac12 \cdot 2\pi r_h = \pi r_h = \textcolor{#00f}{\pi \frac a2}$$

... und die Fläche des Halbkreises nicht

Die Fläche \(F\) eines Kreises mit Radius \(r\) ist \(F=\pi r^2\). Die Fläche \(A_h\) eines Halbkreises ist halb so groß. Hat der Halbkreis den Radius \(r_h=a/2\), so ist seine Fläche: $$A_h = \frac12 \cdot \pi r_h^2 = \textcolor{#f00}{\frac12 \cdot \pi \left( \frac a2 \right)^2}$$

ich habe in der Antwort die zugehörigen Terme farblich markiert.

Answer 2

Hallo

das sind 2 Halbkreise oben mit Radius 4,5, und insgesamt ein Kreisausschnitt  Radius 18 von 120°, wenn du noch angegeben hättest , wie der untere Teil konstruiert ist, als Stücke von Kreisen mit Radius 18

Wenn man das ordentlich konstruiert, die Kreise ganz zeichnet, kann man es auch rechnen, mit deiner unzulännglichen Skizze kannst du natürlich nicht viel rauskriegen.

Gruß lul