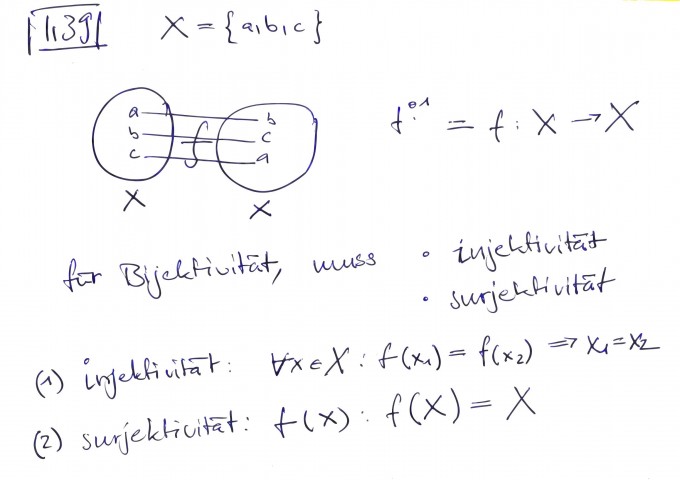
Korrektur im BIld: Surjektion: f(X) = X.
Aufgabe:
Sei X = { a, b, c } eine Menge mit 3 unterschiedlichen Elementen und
f: X -> X
die Funktion definiert durch
f(a) = b
f(b) = c
f(c) = a
Zeigen Sie dass f bijektiv ist.
Was ich weiss:
Für eine Bijektion sind zwei sachen Voraussetzung: Injektion und Surjektion.
- Injektion: f(x1) = f(x2) => x1 = x2, ausserdem müssen wir den Definitionsbereich und Wertebereich kennen.
- Surjektion: f(X) = X. Es gibt kein Element in der Menge das von der Funktion unberührt bleibt.
Problem:
Ich habe es bildlich dargestellt und "sehe", dass f injektiv ist, und surjektiv und folglich auch bijektiv.
Frage:
Aber wie führe ich den Beweis formal ?
Bild: