Schaubild K der gegebenen Funktion f. f(x)= -1/4(x+1)^2 (3-2x)

Question

Hab eine Aufgabe kann mir die jemand mal als Musterlösung ausrechnen?

 

Zeichnen Sie das Schaubild K der gegebenen Funktion f in einem geeigneten Bereich.

Machen Sie Aussagen über den Verlauf K (Umfangreich) mit GTR

f(x)=-1/4(x+1)^2(3-2x)

 

vielen Dank

Comments

Spontan kann man etwas über die Nullstellen sagen, die sind  gut aus der Funktion ablesbar ,

(-1|0) und (3/2| 0)

Answer 1

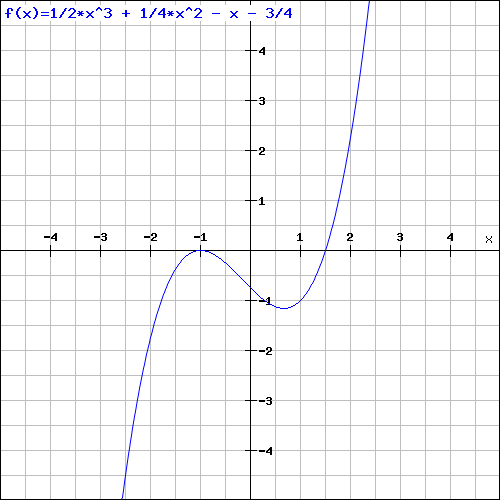
Wir können die Funktion auch ausmultiplizieren zu

f(x) = 1/2*x^3 + 1/4*x^2 - x - 3/4

Jetzt bestimmen wir die Ableitungen

f'(x) = 3/2*x^2 + 1/2*x - 1

f''(x) = 3*x + 1/2

 

Nullstellen f(x) = 0

x = -1 oder x = 1,5

 

Extremstellen f'(x) = 0

x = -1 und x = 2/3

f(-1) = 0 (wussten wir ja schon)

f(2/3) = -125/108 = -1,157

 

Wendestellen f''(x) = 0

x = -1/6 

f(-1/6) = -125/216 = -0,5787

 

Skizze