In welcher Höhe müssen die Striche für die Unterteilungen von 100 Kubikcentimetern angebracht werden?

Question

Ein kegelförmiges GLas mit Radius 5cm und Höhe 15 cm (innenmaße) soll als Messbecher genutzt werden.

In welcher Höhe müssen die Striche für die Unterteilungen von 100 Kubikcentimetern angebracht werden?

Frage steht oben Bitte schnell schreib morgen Klausur

Lg

Answer 1

hi

morgen? also heute? :D

das dürfte ein wenig knapp werden!

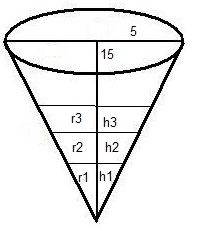
die höhe des ersten teilstrichs ist die höhe eines auf der spitze 'stehenden' kegels mit dem volumen 100ccm

V_Kegel = 100ccm

V_Kegel = 1/3•r²• π•h₁

h₁ = 3•V_Kegel / (r²• π)

2 unbekannte: h₁, r, unbekannt

r₁ / h₁ = 5/15 = 1/3 (siehe bild)

r₁ = h₁/3

h₁ = 3•V_Kegel / (r₁²• π)  r₁ durch h₁/3 ersetzen, nur noch eine unbekannte: h₁

h₁ = 3•V_Kegel  / ((h₁/3)²• π)

h₁ = 3•100ccm  / ((h₁/3)²• π)

h₁= 300ccm  / ((h₁²/9) • π)

h₁ = 9•300ccm  / (h₁² • π)

h₁ = 2700ccm  / (h₁² • π)

h₁³ = 2700ccm / π

h₁ ≈ 13,92477cm das ist die höhe für die erste unterteilung

die höhe h₂ der zweiten unterteilung berechnet sich aus der höhe eines kegelstumpfs mit dem volumen 100ccm

V_Kegelstumpf1 =  h₂ • π / 3 • (R₂² + R•r₂ • r₂²)

100ccm =  h₂ • π / 3 • (R₂² + R•r₂ • r₂²)

2 unbekannte: h₂, r₂

r_{2 /} (h₁ + h₂ ) = 5/15 = 1/3 (siehe bild)

r₂ = (h₁ + h₂ ) / 3

nur noch eine unbekannte: h₂

100ccm =  h₂ • π / 3 • (R₂² + R•r₂ • r₂²)   r₂ durch (h₁ + h₂ ) / 3 ersetzen

100ccm =  h₂ • π / 3 • (R₂² + R•((h₁ + h₂ ) / 3) • ((h₁ + h₂ ) / 3)²)

h₁ ist bekannt, h2 ist unbekannt -> gleichung nach h₂ auflösen. das mache ich jetzt aber nicht mehr, es ist bubu-time! :)

die nächste höhe der markierung ist wieder die höhe eines  kegelstumpfs, ... etc.

viel spaß und erfolg!

Comments

ich habe gerade ein paar fehler verbessert, aber die korrekturen wurden nicht gespeichert! :(

ab hier änderungen:

die höhe h₂ der zweiten unterteilung berechnet sich aus der höhe eines kegelstumpfs mit dem volumen 100ccm

V_Kegelstumpf1 =  h₂ • π / 3 • (R₂² + R₂•r₁ + r₁²)

100ccm =  h₂ • π / 3 • (R₂² + R₂•r₁ + r₁²)

2 unbekannte: h₂, R₂

R_{2 /} (h₁ + h₂ ) = 5/15 = 1/3 (siehe bild, dort ist R₂ als r2 bezeichnet)

R₂ = (h₁ + h₂ ) / 3

 

100ccm =  h₂ • π / 3 • (R₂² + R₂•r₁ + r₁²)   R₂ durch (h₁ + h₂ ) / 3 ersetzen

nur noch eine unbekannte: h₂

100ccm =  h₂ • π / 3 • (((h₁ + h₂ ) / 3)² + ((h₁ + h₂ ) / 3)•r₁ + r₁²)

r₁ lässt sich berechnen, h₁ ist bekannt, h₂ ist unbekannt -> gleichung nach h₂ auflösen. das mache ich jetzt aber aus bekannten gründen nicht mehr! :-)

die nächste höhe der markierung ist wieder die höhe eines  kegelstumpfs, ... etc.

mfg