Wahrscheinlichkeit - Statistik

Question

Hallo ‍♀️

Und zwar komme ich mit folgender Aufgabe nicht zurecht:

Etwa 20% der Deutschen sind blond. Wie groß ist die Wahrscheinlichkeit, dass in einer Schulklasse mit 25 Schülerinnen und Schülern

a) genau 5

b) zwischen 4 und 6

c) höchstens 5

d) mindestens 6

blond sind?

e) Wie viele Blonde erwarten Sie nach der obigen Information in Ihrem Kurs? Prüfen Sie, ob die tatsächliche Anzahl im 2 o-Intervall um den Erwartungswert liegt  

Answer 1

a) P(X=5) = (25über5)*0,2^5*0,8^20

b) P(4<=x<=6) = P(X<=6)-P(X<=3)

c) P(X<=5) = P(X=0)+P(X=1)+...P(X=5)

d) P(X>=6) = 1-P(X<=5)

Answer 2

Benutze die kumulierte Binomialverteilung deines GTR, mit der lassen sich ggf. beliebige Intervallwahrscheinlichkeiten berechnen. Hier die Ausgabe beim TI-Nspire CX:

 

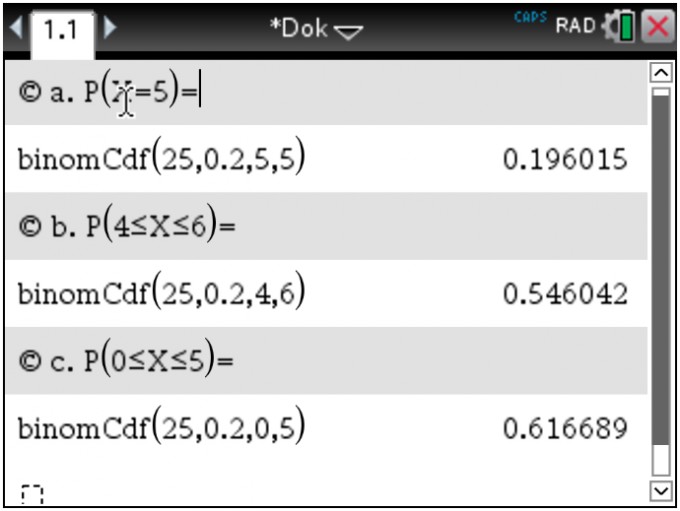
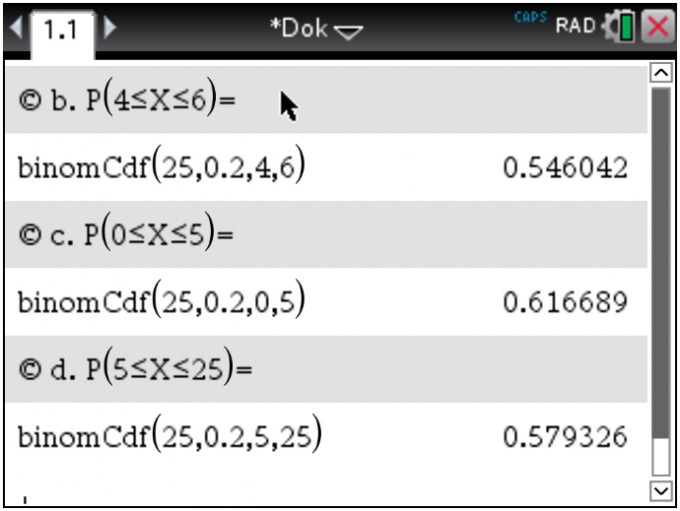
zu e) Es werden \(\mu=n\cdot p\) Blonde im Kurs erwartet, wobei \(n\) die Kursstärke und \(p=0.2\) der Anteil der Blonden in der Grundgesamtheit ist. Liegt die tatsächliche Anzahl im \(2\sigma\)-Intervall um \(\mu\), also im Intervall \(\left[\mu-2\sigma,\mu+2\sigma\right]\)? Berechne \(\sigma=\sqrt{n\cdot p \cdot\left(1-p\right)}\), zähle die Blonden im Kurs und prüfe, ob diese Anzahl im besagten Intervall liegt.