Hallo Markus,
eine gute Skizze ist der Schlüssel zur Lösung:
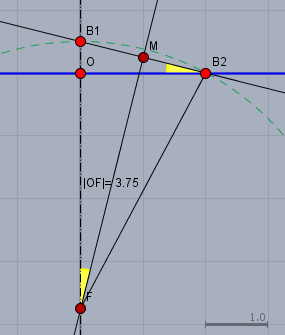
Dort siehst Du die beiden Positionen \(B_1\) und \(B_2\) der Boje, die am Punkt \(F\) am Meeresboden fixiert sein soll. Die Dreiecke \(\triangle OB_2 B_1\) und \(\triangle MB_1F\) sind ähnlich. Folglich ist
$$\frac{|B_1F|}{|B_1 M|} = \frac{|B_1 B_2|}{|OB_1|}$$ Nun ist nach Pythagoras $$|B_1B_2| = \sqrt{0,5^2 + 2^2}\text{m} \approx 2,06 \text{m}$$ und $$|B_1M| = \frac{1}{2} |B_1B_2| \approx 1,03 \text{m}$$ Folglich ist
$$|B_1F| = \frac{|B_1 B_2| \cdot |B_1 M|}{|OB_1|} = \frac{2,06 \text{m} \cdot 1,03 \text{m}}{0,5 \text{m}} = 4,25 \text{m}$$ Der Rest ist einfach. Die Meerestiefe \(|OF|\) ist (nicht tief) $$|OF| = |B_1F| - |B_1O| = 4,25 \text{m} - 0,5 \text{m} = 3,75 \text{m}$$ Gruß Werner