Zerlegen Sie den Vektor a in einen Vektor parallel zum Vektor b

Question

Zerlegen Sie den Vektor \( \vec { a } = \left( \begin{array} { c } { 1 } \\ { 1 } \\ { - 1 } \end{array} \right) \) in einen Vektor \( \vec { a } _ { \| } \) parallel zum Vektor \( \vec { b } = \left( \begin{array} { l } { 1 } \\ { 2 } \\ { 2 } \end{array} \right) \) und einen Vektor \( \vec { a } _ { \perp } \), der senkrecht auf \( \vec { b } \) steht.

Answer 1

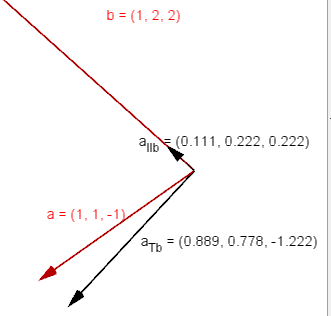
Lass es mich mal so zeigen:

Es gibt einen Vektor (a parallel b) \(a_{IIb}  \) und einen Vektor (a senkrecht b) \( a_{⊥b}\), also

\(a_{IIb} \; a_{⊥b} = b \; a_{⊥b} =0  \) 

Wir wandern ein t-stückchen parallel b = \(a_{IIb} \)= t b bis wir senkrecht abbiegen um an die Spitze von a zu kommen \( a_{⊥b}\) = (a - t b)

===> b (a - t b) =0 ===> t=1/9 ===> \(a_{IIb} \, :=  \, \frac{1}{9} \left( \begin{array}{r}1\\2\\ 2\\ \end{array} \right) \) ==> \(a_{⊥b} \, :=  \,\frac{1}{9} \left( \begin{array}{r}8\\7\\ -11\\ \end{array} \right) \)

mitBild:

Comments

Auf die ergebnisse in der Zeichnung bin ich auch gekommen mit 8/9 = 0,88889 usw. Aber wie kommt man auf:

$$= \frac { 1 } { 9 } \left( \begin{array} { r } { 8 } \\ { 7 } \\ { - 11 } \end{array} \right)$$

---

Wie rechnet man das aus?

Den Vektor \( \vec{ a } _ { \perp } \) erhält man dann mittels:

$$\vec { a } _ { \perp } = \vec { a } - \vec { a } _ { \| } = \left( \begin{array} { c } { 1 } \\ { 1 } \\ { - 1 } \end{array} \right) - \frac { 1 } { 9 } \left( \begin{array} { l } { 1 } \\ { 2 } \\ { 2 } \end{array} \right) = \frac { 1 } { 9 } \left( \begin{array} { c } { 8 } \\ { 7 } \\ { - 11 } \end{array} \right)$$

---

Ich weiß jetzt nicht wirklich, was Du noch hören willst.

Mein Weg führt letztendlich auf die gleiche Rechnung, wie in Deiner Lösung (für a_⊥), deshalb hab sie nicht explizit ausgeschrieben - was ist daran unklar?

---

$$\begin{pmatrix} 1\\1\\-1 \end{pmatrix}-\frac{1}{9}\begin{pmatrix} 1\\2\\2 \end{pmatrix}\\ =\begin{pmatrix} 1-\frac{1}{9}\\1-\frac{2}{9}\\-1-\frac{2}{9} \end{pmatrix}\\ =\begin{pmatrix} \frac{8}{9}\\\frac{7}{9}\\-\frac{11}{9} \end{pmatrix}$$

Jetzt \( \frac{1}{9} \) wieder ausklammern et voilà!

Meintest du das?

---

Meine Antwort bezog sich auf den vorletzten Kommentar und ja, auf die Idee könnte man aufgrund des letzten Kommentars kommen, das man Bruchrechnen erklären sollte. Aber da

>auf die ergebnisse in der zeichnung bin ich auch gekommen mit 8/9 = 0,88889 usw..

sagte er was anderes. Verwirrend...

---

@wächter: Da du schon alles erklärt hattest, fiel mir das als einzige Möglichkeit ein, weil der FS von seinen "Ergebnissen aus der Zeichnung" sprach.

Answer 2

Ansatz:

1                    1
1       =   x *   2           +  a_⊥    
-1                    2

Nach   a⊥    auflösen und dann    a⊥    * a = 0 verwenden gibt

1-x  +  1 -2x  +  1+ 2x = 0    also    x=3.

Damit ist die Zerlegung:

1                    1                 -2
1       =     3*   2           +    -5
-1                    2                 -7

Comments

verstehe leider null wie das gehen soll

die lösung müsste lauten

a) habe ich verstanden ...kein problem

aber b) sch... richtig rein

---

und dann    a⊥    * a = 0 verwenden

\(a_\perp\) soll lt. Aufgabenstellung senkrecht auf \(b\) stehen - also: \(a_\perp \cdot b = 0\)