hier lohnt es sich doch, ein paar Bildchen zu malen:
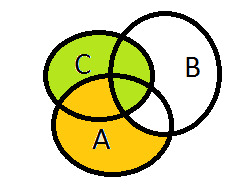
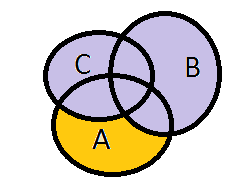
Die orange Fläche der ersten Figur ist \(A \backslash B\). Die Komposition \(M_1 = (A \backslash B) \cup C\) ist dann die gesamte farbige Fläche. In der zweiten Figur ist \(C \cup B\) violett und \(M_2 = A \backslash (B \cup C)\) ist dann nur noch die orange Fläche.
Es ist bereits offensichtlich, dass die Mengen nicht gleich sind. Prüfe das z.B. für ein Element \(x | x \in C \). In der ersten Menge \(M_1\) ist \(x\) enthalten wegen \(\dots \cup C\) und in der zweiten Menge \(M_2\) sicher nicht wegen \( \dots \backslash ( \dots \cup C)\).