Um den Winkel einer Richtung (z.B. der Richtung einer Kante) in 3D - bzw. eines Vektors \(v\) - zu einer Fläche mit Normalenvektor \(n\) zu bestimmen, berechnet man den Winkel \(\alpha\) zwischen den Vektoren aus ihrem Skalarprodukt und ihren Längen $$v \cdot n = |v| \cdot |n| \cdot \cos \alpha\quad \implies \alpha = \arccos{\frac{v \cdot n}{|v| \cdot |n|}}$$ und diesen Winkel zieht man von \(90°\) ab. Man erhält den Winkel \(\varphi\) zwischen \(v\) und der betrachteten Fläche: $$\varphi = 90° - \alpha = 90° - \arccos{\frac{v \cdot n}{|v| \cdot |n|}}$$ ein Bild, um sich das besser vorstellen zu können:
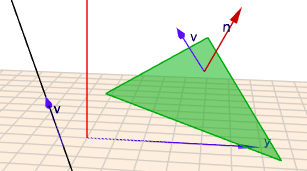
(klick auf das Bild und rotiere die Szene mit der Maus)