Zeichne dir einfach mal die Gegebenheiten in ein eigenes Koordinatensystem. Ich wähle 1 LE = 100 m.
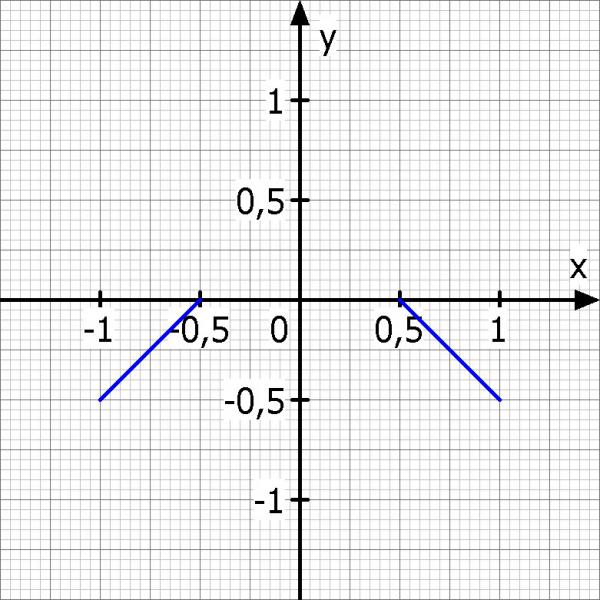
Solange nichts vorgegeben ist bist du in der Wahl des Koordinatensystems frei.
Kannst du die Steigung der beiden blauen Strecken bestimmen? Erinner dich. Die Steigung ist das was du nach oben oder unten gehst, wenn du eine Einheit nach rechts gehst.
Du solltest auf die Steigungen 1 und -1 kommen.
Die Bedingungen lauten hier also
f(0.5) = 0
f'(0.5) = -1
Wenn man es noch Krümmungssprungfrei haben möchte kommt noch
f''(0.5) = 0
als Bedingung hinzu.
Wir haben jetzt 3 Bedingungen, was eine achsensymmetrische Funktion 4. Grades gibt.
f(x) = ax^4 + bx^2 + c
Wir wandeln jetzt die Bedingungen in ein Gleichungssystem um
f(0.5) = 0
a/16 + b/4 + c = 0
f'(0.5) = -1
a/2 + b = -1
f''(0.5) = 0
3·a + 2·b = 0
Wir lösen das Gleichungssystem mit dem Additionsverfahren und erhalten.
a = 1 ∧ b = - 3/2 ∧ c = 5/16
Damit lautet die Gleichung
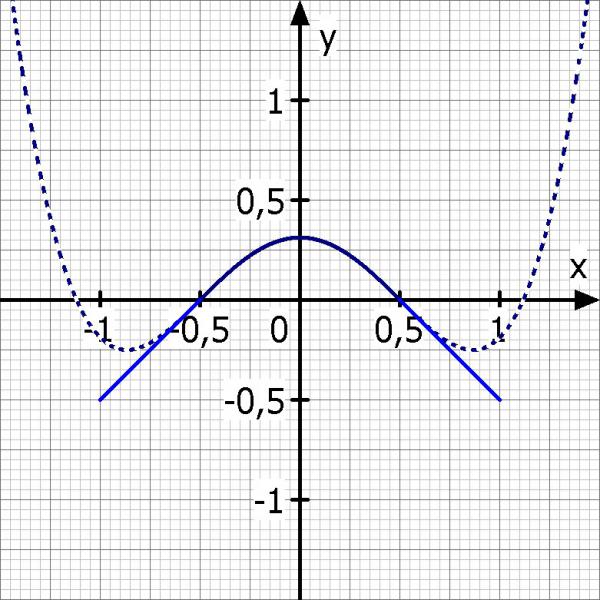
f(x) = x^4 - 3/2·x^2 + 5/16
Ich zeichne die Funktion im Bereich von -0.5 bis 0.5 ebenso ins Koordinatensystem ein.