Näherungswert Bestimmen Vorgehensweise

Question

c) In der Abbildung ist der Graph der Funktion \( k \) mit \( k(x)=-0,3 \cdot x^{2} \cdot e^{-0,2 x} \) für \( 0 \leq x \leq 20 \) dargestellt.

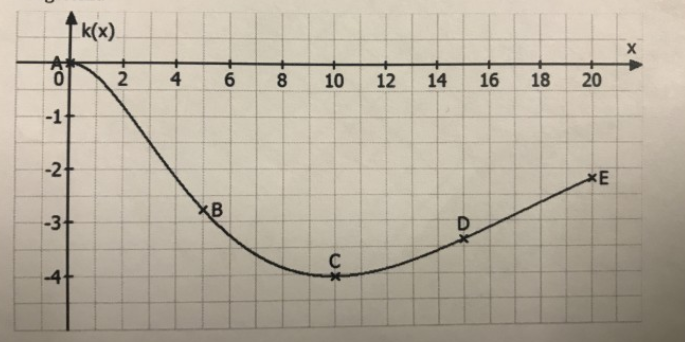
a) verbindet man die Punkte A(0|0), B(5|k(5)), C(10|k(10)), D(15|k(15)) und E(20|k(20)) in dieser Reihenfolge durch strecken, liefert es die Summe der Längen dieser Strecken einen Näherungswert gür die Länge des in der Abbildung dargestellten Graphen von k im Intervall [0;20].

Berechnen Sie diesen Näherungswert.

Ich brauche bloß den Ansatz

b) Beschreiben Sie, wir man unter Verwendung von Strecken zwischen Punkten auf dem in der Abbildung dargestellten Graphen von k im Intervall [0;20] dessen Länge beliebig genau berechnen kann.

Kann man es hier mündlich beschreiben ?

Danke

Answer 1

die Strecke zwischen zwei Punkten in der Ebene - oder in dem Koordinatensystem - wird mit Hilfe des Satzes des Pythagoras berechnet. In der Skizze habe ich mal zwei Punkte eingezeichnet:

Die beiden Punkte haben die Koordinaten \(A(2|2)\) und \(B(6|5)\). Wenn Du nun das markierte Dreieck betrachtest, dann berechnen sich seine Katheten aus den Differenzen der Koordinaten. Die waagerechte Kathete ist \(6-2=4\) und die senkrechte ist \(5-2=3\). Dann gilt nach Pythagoras $$|AB|^2 = 4^2 + 3^2 = 25 \quad \implies |AB| = \sqrt{25} = 5$$ In Deinem konkreten Fall berechnet man eine Strecke \(s_i\) zwischen zwei Punkten \((x_{i-1}|k(x_{i-1}))\) und \((x_{i}|k(x_{i}))\) aus: $$s_i = \sqrt{(x_{i} - x_{i-1})^2 + (k(x_{i}) - k(x_{i-1}))^2}$$

zu b) Du wirst natürlich immer genauer, umso näher die Punkte zusammen rücken. man benötigt also mehr Punkte, die gleichmäßig im Intervall von \([0;20]\) verteilt werden. Das kann man mündlich beschreiben, das kann man auch 'mathematisch' hinschreiben. Die Gesamtstrecke \(S\) ist die Summe aller Teilstrecken \(s_i\). Das \(i\) ist ein Index, der von \(1\) bis \(n\) (der Anzahl der Strecken) läuft: $$S = s_1 + s_2 + s_3 + \dots + s_{n-1} + s_n = \sum_{i=1}^n s_i$$ In Deinem Fall oben war das \(n=4\). Jetzt kann man sich überlegen, wie man zu einem \(s_i\) kommt. Die X-Koordinate von \(x_i\) ist $$x_i = \frac{i}{n} \cdot (b-a) +a$$ wobei \(a\) und \(b\) die Grenzen des Intervalls sind: \(a=0\) und \(b=20\). Die Y-Koordinaten sind dann die Funktionswerte. Und die Differenz zwischen zwei X-Koordinaten ist immer die gleiche, nämlich \(x_i - x_{i-1} = (b-a)/n\). Folglich ist dann der Näherungswert der Streckenlänge $$S = \sum_{i=1}^n s_i = \sum_{i=1}^n \sqrt{\left( \frac {20}n \right)^2 + \left(k \left( 20\frac{i}{n} \right)-k\left(20 \frac{i-1}{n}\right) \right)^2}$$ Gruß Werner

Answer 2

Hallo

 der Abstand =länge der Strecke zwischen 2 Punkten solltest du doch kennen?

P1=(x1,y1), P2=(x2,y2) ,

P1P2=√((x2-x1)^2+(y2-y1)^2)

 also alle die k ausrechnen  und dann die Längen ausrechnen,

2. Teil, mündlich oder schriftlich die Punkt immer dichter nebeneinander setzen. je dichter, desto genauer.

Gruß lul