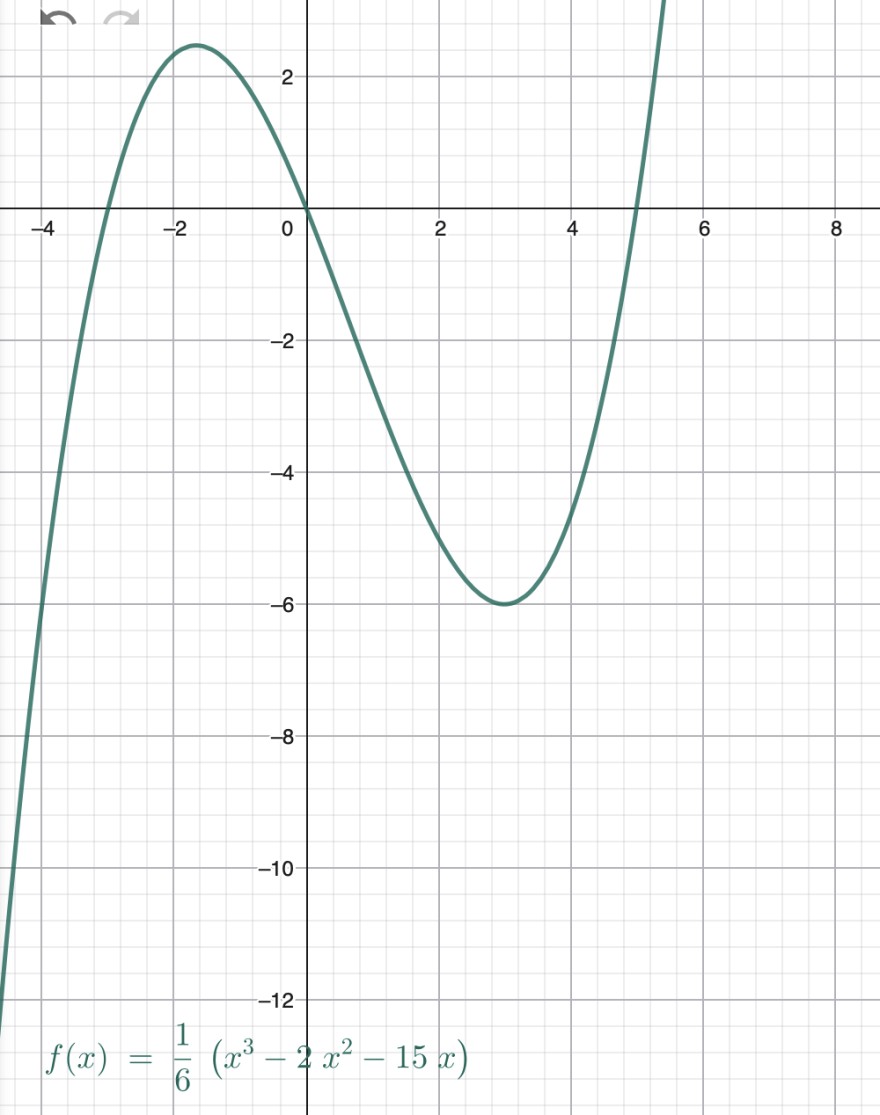
Zu bestimmen ist eine ganzrationale Funktion f(x) vom Grad 3, deren Graph folgende Eigenschaften hat:
T(3 l -6) ist Tiefpunkt; 0 und -3 sind Nullstellen
0 und -3 sind Nullstellen:
Nullstellenform:
\( f(x)=ax(x+3)(x-N)=a(x^3-Nx^2+3x^2-3Nx) \)
An der Stelle x=3 ist ein Tiefpunkt 1.Ableitung
\( f'(x)=a(3x^2-2Nx+6x-3N) \)
\( f'(3)=a(27-6N+18-3N)=a(45-9N)=0\)
\( N=5\)
\( f(x)=a(x^3-5x^2+3x^2-15x)=a(x^3-2x^2-15x)\)
T(3 l -6)
\( f(3)=a(27-18-45)=-36a=-6\)
\(a=\frac{1}{6}\)
\( f(x)=\frac{1}{6}(x^3-2x^2-15x)\)