Hallo Chingo,
Antwort korrigiert
ich habe die drei Vektoren einfach mal im Geoknecht3D eingegeben und die sehen ziemlich abhängig aus.
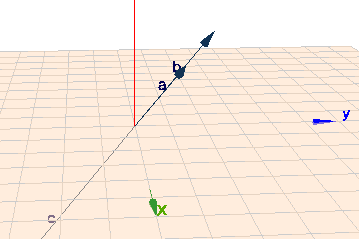
klick auf das Bild und rotiere die Szene mit der Maus. Es hat den Anschein, als ob die drei Vektoren in einer Ebene liegen und folglich linear abhängig sind. Das überprüfe ich nun rechnerisch. Sind sie linear abhängig, so muss es zwei Werte \(r\) und \(s\) geben, die folgende Gleichung erfüllen:
$$\vec{a} \cdot r + \vec{b} \cdot s = \vec{c}$$ bzw. mit Zahlen $$\begin{pmatrix} 12\\4 \\ \cancel{20} 10 \end{pmatrix} \cdot r + \begin{pmatrix} 5\\8 \\ 12 \end{pmatrix} \cdot s = \begin{pmatrix} 16\\-20 \\ \colorbox{#ffff44}{-18} \end{pmatrix}$$ aus den ersten beiden Zeilen berechne ich \(r\) und \(s\) $$\begin{array}{cc|c} 12 & 5 & 16 \\ 4 & 8 & -20\end{array} \\ \begin{array}{cc|c} 0 & -19 & 76 \\ 4 & 8 & -20\end{array} \\ \implies s= -\frac{76}{19} = -4 \\ 4r - 8 \cdot 4 = -20 \\ \implies r = 3 \\$$ Einsetzen des Ergebnis in die dritte Zeile $$10 \cdot 3 + 12 \cdot (-4) = \colorbox{#ffff44}{-18} \quad \text{(s.o.)}$$ d.h. die drei Vektoren sind linear abhängig.
Gruß Werner