Ich brauche eure Hilfe um zu überprüfen ob ich folgende Aufgabe richtig gemacht habe. Sollte dies nicht der Fall sein, wäre ich euch sehr Dankbar falls Ihr mir eine Hilfestellung geben könntet. Ich wäre auch sehr Dankbar falls Ihr mir sagen könntet worauf ich bei der Notation in Zukunft achten soll um meine Beweisführung zu verbessern.
Gegeben ist folgende Aufgabe:
(a) Zeigen Sie unter Verwendung des Skalarproduktes: Für jedes
ebene Dreieck mit Seitenlängen a, b, c und Winkel α, β und γ gilt:
$$a = b*cos(γ ) + c*cos(β )$$
(Bezeichnungen wie in der beistehenden Figur) 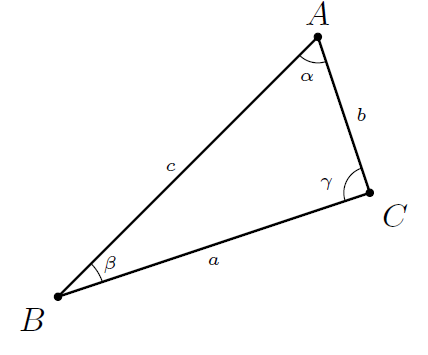
(b)
$$\text{Es seien } (x, y) \in \mathbb{R} \\ \text{Zeigen Sie: } \langle x, y \rangle = \frac{1}{4} (\Vert x+y \Vert^{2}-\Vert x-y \Vert^{2}) \\ \text{,wobei }\langle .; . \rangle \text{ das Skalarprodukt auf }\mathbb{R}^{n} \text{ bezeichnet.}$$
__________
Meine Beweisführung bzw. Überlegung zur (a)
$$\text{Sei } \\\langle x,y \rangle= \Vert x \Vert*\Vert y \Vert * cos( φ) \text{ und } \Vert x \Vert^{2}=x^{2} \text{ definiert} \\ \text{Beweis: } \\ a = b*cos(γ ) + c*cos(β ) \text{ |} *a \\ a^{2}=a*b*cos(γ ) + a*c*cos(β ) \text{ |} \Vert \\ \Vert a^{2} \Vert= \Vert a\Vert \Vert b\Vert cos(γ)+\Vert a\Vert \Vert c\Vert cos(β) \\ a^{2}= \langle a,b \rangle+\langle a,c \rangle \\ a=\sqrt{\langle a,b \rangle+\langle a,c \rangle}$$
Meine Überlegung zur (b)
$$ \langle x, y \rangle = \frac{1}{4} (\Vert x+y \Vert^{2}-\Vert x-y \Vert^{2}) \\\langle x, y \rangle = \frac{1}{4} ( x^{2}+2xy+y ^{2}- x^{2}+2xy-y^{2})) \\ \langle x, y \rangle = \frac{1}{4} (4xy) \\\langle x, y \rangle = \langle x,y \rangle$$