Aufgabe:
Im Dreieck ABC hat die Winkelhalbierende wBeta die Steigung m.
Zeichne das Dreieck ABC und berechne die fehlenden Seitenlängen und Winkelmaße
a) A ( 2 l 1 ) ; B ( 7 l 1 ) ; a=5LE ; m=-1/2
b) A ( -1 l 2 ) ; B ( 6 l 0 ) ; a=5,3LE ; m=-2
Lösungen ( nur Maßzahlen): 63,4 4,5 5 53,1 63,4 7,3 9,4 95,0 34,2 50,8 7,8
Problem/Ansatz:
geg: a=5LE ; m=-0,5
a) AB= sqrt(7-2)²+(1-1)²
AB=5LE
weiter weiß ich leider nicht weiter, ich hoffe ihr könnt mir hier helfen.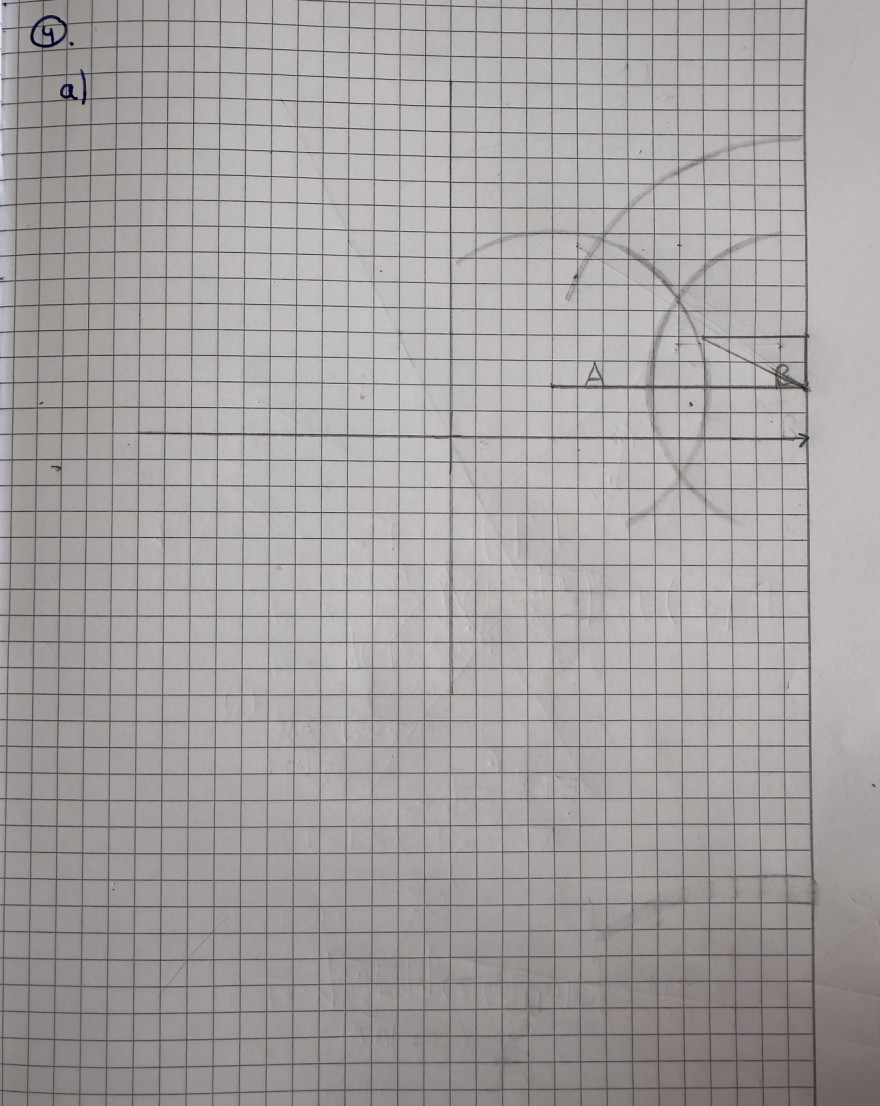
Text erkannt:
(4)
a)